Empirical Data-Driven Linear Model of a Swimming Robot Using the Complex Delay-Embedding DMD Technique

Abstract

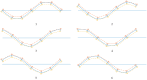
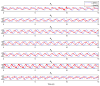
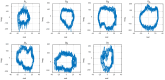
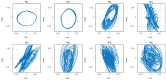
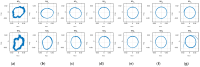
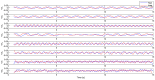
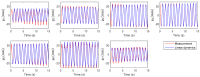
Anguilliform locomotion, an efficient aquatic locomotion mode where the whole body is engaged in fluid-body interaction, contains sophisticated physics. We hypothesized that data-driven modeling techniques may extract models or patterns of the swimmers' dynamics without implicitly measuring the hydrodynamic variables. This work proposes empirical kinematic control and data-driven modeling of a soft swimming robot. The robot comprises six serially connected segments that can individually bend with the segmental pneumatic artificial muscles. Kinematic equations and relations are proposed to measure the desired actuation to mimic anguilliform locomotion kinematics. The robot was tested experimentally and the position and velocities of spatially digitized points were collected using QualiSys^® Tracking Manager (QTM) 1.6.0.1. The collected data were analyzed offline, proposing a new complex variable delay-embedding dynamic mode decomposition (CDE DMD) algorithm that combines complex state filtering and time embedding to extract a linear approximate model. While the experimental results exhibited exotic curves in phase plane and time series, the analysis results showed that the proposed algorithm extracts linear and chaotic modes contributing to the data. It is concluded that the robot dynamics can be described by the linearized model interrupted by chaotic modes. The technique successfully extracts coherent modes from limited measurements and linearizes the system dynamics.

Keywords: CDE DMD; bio-inspired locomotion; bio-robotics; data-driven modeling; soft robotics.

Figure A1

The measurement setup.

Figure 1

Geometrical model of the robotic fish. The solid lines represent the robot backbone midline, and the dashed lines show the actuators’ nominal axes.

Figure 2

Mechanical drawings: (a) 3D model of the robot; (b) the segmental assembly parts and balancing bladders.

Figure 3

Geometrical representation of the desired actuator lengths calculations with a wave traveling left to right from 1 to 6. The blue curve represents the robot backbone axis versus the initial state, i.e., the straight blue line. The dashed lines represent the soft actuators’ axes.

Figure 4

The experimental data. The robot’s undulation period is 1.1 s.

Figure 5

Phase plot of the experimental data.

Figure 6

Phase plot of the dynamic variables with d = 30.

Figure 7

Phase plot of the dynamic variables with d = 110.

Figure 8

Evolution of the first two modes with embedding dimension: (a) Standard DMD; (b) CDE DMD with d = 30; (c) d = 60; (d) d = 85; (e) d = 110; (f) d = 140; (g) d = 170.

Figure 9

Conceptualization of the linearization technique. Measurement data are projected to the CDE coordinates, in the encoding stage. Consequently, the linear (and nonlinear) portion is obtained by superimposing the linear (and nonlinear chaotic) modes, in the decoding stage.

Figure 10

Time-series plot of the CDE dynamic variables with d = 110.

Figure 11

The linearized model versus the measured data.

Figure 12

Comparison of the reconstructed data, the nonlinearity contribution, and the measurements.

Figure 13

Comparison of the CDE DMD results with the original data.

Figure 14

Data with injected noise: (a) The original and corrupted data; (b) Histogram of the added noise.

Figure 15

Comparison of the dynamic variables of the original (top) and the corrupted (bottom) data.

Figure 16

Comparison of the CDE DMD results with the noisy data.