Computer Simulations of the Temperature Dependence of Enzyme Reactions
- PMID: 39884967
- PMCID: PMC11823412
- DOI: 10.1021/acs.jctc.4c01733
Computer Simulations of the Temperature Dependence of Enzyme Reactions
Abstract
In this review we discuss the development of methodology for calculating the temperature dependence and thermodynamic activation parameters for chemical reactions in solution and in enzymes, from computer simulations. We outline how this is done by combining the empirical valence bond method with molecular dynamics free energy simulations. In favorable cases it turns out that such simulations can even capture temperature optima for the catalytic rate. The approach turns out be very useful both for addressing questions regarding the roles of enthalpic and entropic effects in specific enzymes and also for attacking evolutionary problems regarding enzyme adaptation to different temperature regimes. In the latter case, we focus on cold-adaptation of enzymes from psychrophilic species and show how computer simulations have revealed the basic mechanisms behind such adaptation. Understanding these mechanisms also opens up the possibility of designing the temperature dependence, and we highlight a recent example of this.
Conflict of interest statement
The authors declare no competing financial interest.
Figures

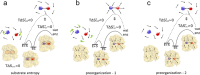
 ) is dominated by reorientation of the substrates,
then the enzyme could pay the penalty already when binding them in
a reactive orientation (
) is dominated by reorientation of the substrates,
then the enzyme could pay the penalty already when binding them in
a reactive orientation ( and
and  ). (b) If
). (b) If  is dominated by reorientation of water
molecules, then the enzyme could bind the substrates in a preorganized
active site that does not need reorientation of the protein dipoles
(
is dominated by reorientation of water
molecules, then the enzyme could bind the substrates in a preorganized
active site that does not need reorientation of the protein dipoles
( ). (c) If the uncatalyzed reaction
has similarly small charge separation in the reactant and transition
states, then the enzyme could yield a favorable activation entropy
by stabilizing a more polar reactant state, causing a relaxation of
the aligned protein dipoles in the transition state (
). (c) If the uncatalyzed reaction
has similarly small charge separation in the reactant and transition
states, then the enzyme could yield a favorable activation entropy
by stabilizing a more polar reactant state, causing a relaxation of
the aligned protein dipoles in the transition state ( ).
).



Similar articles
-
Towards Rational Computational Engineering of Psychrophilic Enzymes.Sci Rep. 2019 Dec 16;9(1):19147. doi: 10.1038/s41598-019-55697-4. Sci Rep. 2019. PMID: 31844096 Free PMC article.
-
Computer simulations explain the anomalous temperature optimum in a cold-adapted enzyme.Nat Commun. 2020 May 26;11(1):2644. doi: 10.1038/s41467-020-16341-2. Nat Commun. 2020. PMID: 32457471 Free PMC article.
-
Entropy and Enzyme Catalysis.Acc Chem Res. 2017 Feb 21;50(2):199-207. doi: 10.1021/acs.accounts.6b00321. Epub 2017 Feb 7. Acc Chem Res. 2017. PMID: 28169522
-
Hybrid schemes based on quantum mechanics/molecular mechanics simulations goals to success, problems, and perspectives.Adv Protein Chem Struct Biol. 2011;85:81-142. doi: 10.1016/B978-0-12-386485-7.00003-X. Adv Protein Chem Struct Biol. 2011. PMID: 21920322 Review.
-
Temperature, Dynamics, and Enzyme-Catalyzed Reaction Rates.Annu Rev Biophys. 2020 May 6;49:163-180. doi: 10.1146/annurev-biophys-121219-081520. Epub 2020 Feb 4. Annu Rev Biophys. 2020. PMID: 32040931 Review.
References
-
- Warshel A.Computer Modeling of Chemical Reactions in Enzymes and Solutions; John Whiley & Sons: New York, 1991.
-
- Bruice T. C.; Lightstone F. C. Ground state and transition state contributions to the rates of intramolecular and enzymatic reactions. Acc. Chem. Res. 1999, 32, 127–136. 10.1021/ar960131y. - DOI
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources
