High-dimensional, outcome-dependent missing data problems: Models for the human loci
- PMID: 39885761
- PMCID: PMC11951372
- DOI: 10.1177/09622802241304112
High-dimensional, outcome-dependent missing data problems: Models for the human loci
Abstract
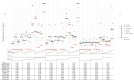
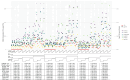
Missing data problems are common in biological, high-dimensional data, where data can be partially or completely missing. Algorithms have been developed to reconstruct the missing values by means of imputation or expectation-maximization algorithms. For missing data problems, it has been suggested that the regression model of interest should be incorporated into the imputation procedure to reduce bias of the regression coefficients. We here consider a challenging missing data problem, where diplotypes of the KIR loci are to be reconstructed. These loci are difficult to genotype, resulting in ambiguous genotype calls. We extend a previously proposed expectation-maximization algorithm by incorporating a potentially high-dimensional regression model to model the outcome. Three strategies are evaluated: (1) only allelic predictors, (2) allelic predictors and forward-backward selection on haplotype predictors, and (3) penalized regression on a saturated model. In a simulation study, we compared these strategies with a baseline expectation-maximization algorithm without outcome model. For extreme choices of effect sizes and missingness levels, the outcome-based expectation-maximization algorithms outperformed the no-outcome expectation-maximization algorithm. However, in all other cases, the no-outcome expectation-maximization algorithm performed either superior or comparable to the three strategies, suggesting the outcome model can have a harmful effect. In a data analysis concerning death after allogeneic hematopoietic stem cell transplantation as a function of donor KIR genes, expectation-maximization algorithms with and without outcome showed very similar results. In conclusion, outcome based missing data models in the high-dimensional setting have to be used with care and are likely to lead to biased results.
Keywords: KIR genes; Missing data; expectation-maximization algorithm; haplotype reconstruction; multiple imputation; outcome dependent imputation.
Conflict of interest statement
Declaration of conflicting interestsThe author(s) declared no potential conflicts of interest with respect to the research, authorship and/or publication of this article.
Figures



Similar articles
-
Haplotype reconstruction for genetically complex regions with ambiguous genotype calls: Illustration by the KIR gene region.Genet Epidemiol. 2024 Feb;48(1):3-26. doi: 10.1002/gepi.22538. Epub 2023 Oct 13. Genet Epidemiol. 2024. PMID: 37830494
-
Accuracy of haplotype frequency estimation for biallelic loci, via the expectation-maximization algorithm for unphased diploid genotype data.Am J Hum Genet. 2000 Oct;67(4):947-59. doi: 10.1086/303069. Epub 2000 Aug 22. Am J Hum Genet. 2000. PMID: 10954684 Free PMC article.
-
Estimation of German KIR Allele Group Haplotype Frequencies.Front Immunol. 2020 Mar 12;11:429. doi: 10.3389/fimmu.2020.00429. eCollection 2020. Front Immunol. 2020. PMID: 32226430 Free PMC article.
-
An empirical comparison of some missing data treatments in PLS-SEM.PLoS One. 2024 Jan 19;19(1):e0297037. doi: 10.1371/journal.pone.0297037. eCollection 2024. PLoS One. 2024. PMID: 38241223 Free PMC article. Review.
-
Algorithms for inferring haplotypes.Genet Epidemiol. 2004 Dec;27(4):334-47. doi: 10.1002/gepi.20024. Genet Epidemiol. 2004. PMID: 15368348 Review.
References
-
- Heitjan DF, Rubin DB. Ignorability and coarse data. Ann Stat 1991; 19: 2244–2253.
-
- Little RJA, Rubin DB. Statistical Analysis With Missing Data. 3rd ed. Hoboken, NJ: Wiley, 2020.
-
- Moons KGM, T. Donders RAR, Stijnen T, et al.. Using the outcome for imputation of missing predictor values was preferred. J Clin Epidemiol 2006; 59: 1092–1101. - PubMed
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

