Bias Dependence of the Transition State of the Hydrogen Evolution Reaction
- PMID: 39900519
- PMCID: PMC11826909
- DOI: 10.1021/jacs.4c18638
Bias Dependence of the Transition State of the Hydrogen Evolution Reaction
Abstract
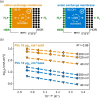
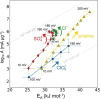
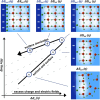
The hydrogen evolution reaction (HER) is one of the most prominent electrocatalytic reactions of green energy transition. However, the kinetics across materials and electrolyte pH and the impact of hydrogen coverage at high current densities remain poorly understood. Here, we study the HER kinetics over a large set of nanoparticle catalysts in industrially relevant acidic and alkaline membrane electrode assemblies that are only operated with pure water humidified gases. We discover distinct kinetic fingerprints between the iron triad (Fe, Ni, Co), coinage (Au, Cu, Ag), and platinum group metals (Ir, Pt, Pd, Rh). Importantly, the applied bias changes not only the activation energy (EA) but also the pre-exponential factor (A). We interpret these changes as entropic changes in the interfacial solvent that differ between acid and base and entropic changes on the surface due to a changing hydrogen coverage. Finally, we observe that anions can induce Butler-Volmer behavior for the coinage metals in acid. Our results provide a new foundation to understand HER kinetics and, more broadly, highlight the pressing need to update common understanding of basic concepts in the field of electrocatalysis.
Conflict of interest statement
The authors declare no competing financial interest.
Figures



Similar articles
-
Electrocatalytic reduction of nitrate ions in neutral medium at coinage metal-modified platinum electrodes.Environ Sci Pollut Res Int. 2023 Mar;30(12):34904-34914. doi: 10.1007/s11356-022-24372-z. Epub 2022 Dec 16. Environ Sci Pollut Res Int. 2023. PMID: 36525190
-
First-principles Density Functional Theory Elucidation of the Hydrogen Evolution Reaction on TM-promoted TiC2 (TM=Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, Pt, and Au).Chemphyschem. 2023 Apr 17;24(8):e202200823. doi: 10.1002/cphc.202200823. Epub 2023 Jan 16. Chemphyschem. 2023. PMID: 36646626
-
Catalytic Surface Specificity of Ni(OH)2 -Decorated Pt Nanocubes for the Hydrogen Evolution Reaction in an Alkaline Electrolyte.ChemSusChem. 2019 Sep 6;12(17):4021-4028. doi: 10.1002/cssc.201901539. Epub 2019 Aug 13. ChemSusChem. 2019. PMID: 31286683
-
Optimizing Pt-Based Alloy Electrocatalysts for Improved Hydrogen Evolution Performance in Alkaline Electrolytes: A Comprehensive Review.ACS Nano. 2023 Nov 14;17(21):20804-20824. doi: 10.1021/acsnano.3c05810. Epub 2023 Nov 3. ACS Nano. 2023. PMID: 37922197 Review.
-
Insight Into Intermediate Behaviors and Design Strategies of Platinum Group Metal-Based Alkaline Hydrogen Oxidation Catalysts.Adv Mater. 2025 Jan;37(4):e2414628. doi: 10.1002/adma.202414628. Epub 2024 Nov 19. Adv Mater. 2025. PMID: 39558771 Review.
Cited by
-
Transition state tuning with concentrated electrolytes.Nat Chem. 2025 Aug;17(8):1146-1147. doi: 10.1038/s41557-025-01882-0. Nat Chem. 2025. PMID: 40702129 No abstract available.
-
Interfacial solvation pre-organizes the transition state of the oxygen evolution reaction.Nat Chem. 2025 Sep 3. doi: 10.1038/s41557-025-01932-7. Online ahead of print. Nat Chem. 2025. PMID: 40903497
References
-
- No̷rskov J. K.; et al. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 152, J23.10.1149/1.1856988. - DOI
-
- Ooka H.; Huang J.; Exner K. S. The Sabatier Principle in Electrocatalysis: Basics, Limitations, and Extensions. Front. Energy Res. 2021, 9, 65446010.3389/fenrg.2021.654460. - DOI
LinkOut - more resources
Full Text Sources

