Non-Markovian quantum exceptional points

Abstract

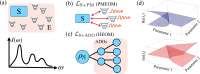
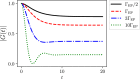
Exceptional points (EPs) are singularities in the spectra of non-Hermitian operators where eigenvalues and eigenvectors coalesce. Open quantum systems have recently been explored as EP testbeds due to their non-Hermitian nature. However, most studies focus on the Markovian limit, leaving a gap in understanding EPs in the non-Markovian regime. This work addresses this gap by proposing a general framework based on two numerically exact descriptions of non-Markovian dynamics: the pseudomode equation of motion (PMEOM) and the hierarchical equations of motion (HEOM). The PMEOM is particularly useful due to its Lindblad-type structure, aligning with previous studies in the Markovian regime while offering deeper insights into EP identification. This framework incorporates non-Markovian effects through auxiliary degrees of freedom, enabling the discovery of additional or higher-order EPs that are inaccessible in the Markovian regime. We demonstrate the utility of this approach using the spin-boson model and linear bosonic systems.

Fig. 1. Schematic illustration depicting EPs for a generic non-Markovian open-system model.

a Generic system-environment model where the structured environment is captured by the spectral density function J(ω). For a given spectral density function and the corresponding environmental correlation function, the exact non-Markovian dynamics can either be described by b the PMEOM or c the HEOM with the corresponding extended Liouvillian superoperators: ${\mathcal{L}}_{\mathrm{S}+\mathrm{PM}}$ and ${\mathcal{L}}_{\mathrm{S}+\mathrm{ADO}}$. d The non-Markovian EPs can then be identified by observing the complex spectrum {λ_i} of these extended Liouvillian superoperators.

Fig. 2. EPs for the spin-boson model.

a Lorentzian J_L(ω) and band gap J_q(ω) spectral densities centered at the qubit transition frequency ${\omega }_0$. d The effects of these spectral densities can be represented by two PMs: The Lorentzian spectral density can be described by the upper PM with qubit-PM coupling strength ${\alpha }_1=\sqrt{\Gamma \Lambda /2}$ and PM’s damping rate γ₁ = 2Λ, while the band gap is characterized by the lower PM with the non-Hermitian coupling ${\alpha }_2=i\sqrt{q\Gamma \Lambda /2}$ and damping rate γ₂ = 2qΛ, where the red dashed line signifies the unphysical nature of this PM. b, c The real and imaginary parts of the spectrum of the extended Liouvillian for the gapless scenario (q = 0). Two EPs, EP2 and an EP3 emerge at the coupling strength Γ = Λ/2. e, f The real and imaginary parts of the spectrum of the extended Liouvillian with q = 1/4. The EP criterion becomes Γ = (1 − q)Λ/2. The dotted curves in b, c, e, f represent the spectrum of the extended superoperators for HEOM (see Supplementary Information for detailed derivations).

Fig. 3. Dynamics of the decoherence function ∣G(t)∣ for different values of the coupling strength Γ.

Here, Γ_EP = (1 − q)Λ/2, and we set Λ = 1 and q = 1/4.

Fig. 4. EP2 and EP3 curves for the two-coupled-modes model.

Real part of the eigenvalues λ_i (i = 1, 2, 3), corresponding to the effective Hamiltonian described in Eq. (29), as a function of the spectral width Λ and coupling strength χ. Here, we set Γ = 1. The yellow and white dashed curves represent the EP2 and EP3 curves, respectively.