Multi-strain phage induced clearance of bacterial infections

Abstract

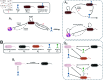
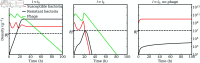
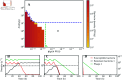
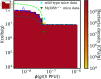
Bacteriophage (or 'phage' - viruses that infect and kill bacteria) are increasingly considered as a therapeutic alternative to treat antibiotic-resistant bacterial infections. However, bacteria can evolve resistance to phage, presenting a significant challenge to the near- and long-term success of phage therapeutics. Application of mixtures of multiple phages (i.e., 'cocktails') has been proposed to limit the emergence of phage-resistant bacterial mutants that could lead to therapeutic failure. Here, we combine theory and computational models of in vivo phage therapy to study the efficacy of a phage cocktail, composed of two complementary phages motivated by the example of Pseudomonas aeruginosa facing two phages that exploit different surface receptors, LUZ19v and PAK_P1. As confirmed in a Luria-Delbrück fluctuation test, this motivating example serves as a model for instances where bacteria are extremely unlikely to develop simultaneous resistance mutations against both phages. We then quantify therapeutic outcomes given single- or double-phage treatment models, as a function of phage traits and host immune strength. Building upon prior work showing monophage therapy efficacy in immunocompetent hosts, here we show that phage cocktails comprised of phage targeting independent bacterial receptors can improve treatment outcome in immunocompromised hosts and reduce the chance that pathogens simultaneously evolve resistance against phage combinations. The finding of phage cocktail efficacy is qualitatively robust to differences in virus-bacteria interactions and host immune dynamics. Altogether, the combined use of theory and computational analysis highlights the influence of viral life history traits and receptor complementarity when designing and deploying phage cocktails in immunocompetent and immunocompromised hosts.

Fig 1. Schematic of mathematical model of phage therapy.

A) Ecological interactions between bacteria, phage and immune system (graphical and mathematical symbols in the legend box). Subpanel A₁ shows the interactions in the simple phage therapy model in a signaling deficient host introduced in Section “Infection model of interacting phage, multi-strain bacteria and non-responsive host immune system”, whereas Subpanel A₂ sketches the addition of more complex dynamics in the model introduced in Section "Structured model for single-phage treatment of in vivo infections with a modulated responsive immune system", namely a structured bacteria population including stages of phage infection and the active recruitment of the host immune cells. Panel B) gathers the cross-infection and mutation networks between specific phage and bacteria strains (listed in the legend box) in the different treatment models. Subpanel B₁ sketches the single-phage treatment structure used in Sections "Infection model of interacting phage, multi-strain bacteria and non-responsive host immune system" and "Structured model for single-phage treatment of in vivo infections with a modulated responsive immune system", whereas B₂ summarizes the cross-infection structure in the phage-cocktail treatment models introduced in Sections "Model of a phage combination therapy against multiple pathogenic bacteria strains" and "Multi-phage treatment model, modulating the evolutionary interactions between bacteria and phage strains during infections" (top and bottom respectively). The main model parameters studied in this work, the immune strength I and the phage adsorption rate ϕ, are colored in red. Arrow types encode the different kind of dynamical interactions (growth, killing, decay, mutations), with dashed-dotted lines indicating saturating nonlinear rates of the form $f(\cdot )\propto \frac{\cdot }{\cdot +C}$. Created in BioRender. NGUYEN NGOC MINH, C. (2025) https://BioRender.com/y51s627

Fig 2. Phage-immune synergy in face of phage resistance.

Simulated dynamics for phage, susceptible and resistant bacteria, when the immune system strength is below $I_0$ (left panel) or above (center, right panels), with phage (left, center) or without (right). Increasing the immune system strength above $I_0$, with $B_I^U>0$, phage can drive susceptible bacteria below $B_I^U$ before the resistant type grows, driving a transition from therapy failure to success (left to center panel). This is a signature of phage-immune synergy as the infection would persist without phage (right). Simulation parameters are reported in Table 1 with $\varphi =10^{002D11}$ g/(h PFU), $I=1.5\cdot 10^7$ and $2.9\cdot 10^7$ cells/g respectively in the left and the other two panels.

Fig 3. Bacteria density as a function of immune strength and phage adsorption rate.

Numerical simulations of the model in Eq. (1) varying I and ϕ. The color map represents the density of bacteria in the last part of the numerical simulations. Single-phage therapy works such that bacteria are driven to elimination with a strong enough immune system (denoted in the white region). Efficient phage (higher ϕ) broaden the therapy success conditions. The analytic condition in Eq. (7) (blue dashed line) accurately predicts the therapy outcome transition. The two black triangles correspond to the left and central panel in Fig 2. Simulation parameters are reported in Table 1.

Fig 4. Phage cocktail therapy succeeds for a wide parameters range.

A) Numerical simulations of the model in Eq. (2) varying I and ϕ. The color map represents the density of bacteria in the last part of the numerical simulations. Adding a second phage clears the infection for a much wider parameter range compared to single-phage treatment, if phages have high enough ϕ, as highlighted by the comparison with the transition for single-phage therapy success in Eq. (7) (blue dashed line). The vertical dashed green line represents the value of ${\varphi }_c$ obtained solving Eq. (8) with Ω = 10 The black annotations correspond to the parameters yielding the population dynamics in panels B),C),D) respectively that show the evolution of phage and bacteria strains during the simulated infection. Simulation parameters are reported in Table 1.

Fig 5. Single-phage therapy succeeds against phage resistance with a strong enough immune system.

Numerical simulations of the model in Eq. (3) varying I and ϕ. The color map represents the density of bacteria in the last part of the numerical simulations, where the white region denotes bacteria clearance. Single-phage therapy works with a strong enough immune system, which needs to be even stronger with inefficient phages (lower ϕ) . The analytic condition in Eq. (9) (blue dashed line) predicts well the therapy outcome transition. The two triangle markers correspond to the I and ϕ inferred in [16] on a model without infected bacteria classes from in vivo experiments, for wild-type (immunocompetent, upward light-blue triangle) and MyD88^-∕- (immunodeficient, downward dark-green triangle) mice. The green (grey) dashed line represents Eq. (9) with a 3-fold increase (decrease) in the concentration of bacteria at the beginning of the therapy. The bigger the bacteria inoculum (worse infection), the harder it is to clear the infection using phage with moderate to low ϕ. Simulation parameters are reported in Table 2.

Fig 6. Efficient phage cocktails improve therapy success in an in vivo model of immunocompromised hosts.

Numerical simulations of the model in Eq. (4) varying I and ϕ, with p = 1. The color map represents the density of bacteria in the last part of the numerical simulations, where the white region denotes bacteria clearance. Phage cocktails can drive bacteria to extinction in immunocompromised hosts provided that phages have a high enough adsorption rate ϕ. The dashed lines show Eq. (11) for p = 0, 0 . 5 and 1 (blue, yellow, green), which agrees well with the simulation results. The black dashed line shows Eq. (10), representing therapy success when bacteria do not develop phage resistance. The two triangle markers correspond to the I and ϕ inferred in [16] from in vivo experiments, for wild-type (immunocompetent, upward light-blue triangle) and MyD88^-∕- (immunodeficient, downward dark-green triangle) mice. Simulation parameters are reported in Table 2.