A detailed theory of thalamic and cortical microcircuits for predictive visual inference

Abstract

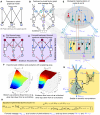
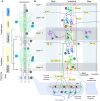
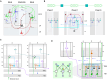
Understanding cortical microcircuitry requires theoretical models that can tease apart their computational logic from biological details. Although Bayesian inference serves as an abstract framework of cortical computation, precisely mapping concrete instantiations of computational models to biology under real-world tasks is necessary to produce falsifiable neural models. On the basis of a recent generative model, recursive cortical networks, that demonstrated excellent performance on vision benchmarks, we derive a theoretical cortical microcircuit by placing the requirements of the computational model within biological constraints. The derived model suggests precise algorithmic roles for the columnar and laminar feed-forward, feedback, and lateral connections, the thalamic pathway, blobs and interblobs, and the innate lineage-specific interlaminar connectivity within cortical columns. The model also explains several visual phenomena, including the subjective contour effect and neon-color spreading effect, with circuit-level precision. Our model and methodology provides a path forward in understanding cortical and thalamic computations.

Fig. 1.. Different approaches to decipher cortical microcircuits.

(A) A visualization of reconstructed cortical neurons shows the formidable complexity in understanding their functional logic. (Image credit: M. Oberlaender). (B) A diagram that summarizes cortical connections [reproduced with permission from (58)]. The summary is a useful sketch that does not correspond to a functional model. (C) Illustration of the triangulation methodology followed in this paper. The brain, the world, and computer science provide partial clues that can be used to construct an overall algorithmic model. The algorithmic model, along with neuroscience data, is then used to derive a functional circuit model. Just like the different pieces in a jigsaw puzzle constrain each other, the combination of algorithmic model and neuroscience data serve to constrain the space of microcircuit instantiations. (D) Examples of questions that can be asked and answered with a functional mathematical theory of cortical circuits. This paper answers those questions, and more.

Fig. 2.. Structure of recursive cortical networks (RCN).

(A) A compositional hierarchy generates the contours of an object, and a Markov random field (MRF) generates its surface appearance. (B) Contour hierarchy consists of features, pools, and laterals. Two subnetworks at the same level of the contour hierarchy keep separate lateral connections by making parent-specific copies of child features and connecting them with parent-specific laterals; nodes within the green rectangle are copies of the feature marked “b.” (C) A three-level RCN representing the contours of a square. Features at level 2 represent the four corners, and each corner is represented as a conjunction of four line-segment features. (D) Inference is achieved by passing messages along forward, backward, and lateral directions. (E) The surface appearance MRF. (F) Forward pass identifies object hypotheses in the scene, and backward and lateral pass segments it from the background for analysis by synthesis. Local hallucinations, e.g., the “v” in (iii), are explained away during parsing to obtain a global solution that best explains the evidence.

Fig. 3.. Neuronal mapping of message-passing in the “Noisy-OR” probabilistic graphical model (PGM), which is a part of recursive cortical networks (RCN) that represents how features and their components interact.

(A) The Noisy-OR PGM with parent nodes representing features, and child nodes representing pixels. The multi-parent interactions at child nodes are modeled by the OR function. (B to D) Factor graph representation of the PGM in (A), with different message annotations. Corresponding to each edge, there are two belief propagation (BP) messages, one in each direction. Nodes consume the incoming messages to produce output messages. (C) First forward pass copies the bottom-up evidence to parent nodes. (D) Subsequent backward-forward passes produce explaining-away competition between parent features. (E) Neural implementation of message-passing in nodes b and e. (F) $m_{d\to a}$ as a function of $m_{e\to d}$ and $m_{b\to d}$ shows the excitatory-inhibitory interactions between the inputs. (G) Details of computation within an excitatory-inhibitory pair of neurons in d, to calculate $m_{d\to a}$ based on the BP equation in (H).

Fig. 4.. Stages of mapping recursive cortical networks (RCN) inference to cortical implementation.

(A) Detailed factor graph of an RCN level. Thin horizontal lines indicate messages at different stages of inference, and these map to different laminae in a biological implementation. Variables and messages in a vertical slice as marked map to computations within a cortical column. (B) Conceptual cortical implementation of message passing. Messages in the different directions along the edge of a probabilistic graphical model (PGM) are implemented in biology using two different sets of neurons for features, laterals, and pools. Messages between different levels go through a stage that includes explaining away and gating. (C) Cortical column as a binary random variable that represents a feature or a concept, for example, an oriented line segment in V1 or the letter B, in IT. The different laminae in a column correspond to the inference computations that determine the participation of this feature in different contexts: laterally in the context of other features at the same level, hierarchically in the context of parent features, hierarchically as context for child features, and pooling/un-pooling for invariant representations.

Fig. 5.. Belief propagation (BP) message computations in recursive cortical networks (RCN) factors and nodes.

(A to E) All computations are in the log domain. Equations with a temperature T can do marginalization (T = 1), maximization (T = 0), or a soft maximization depending on the temperature setting. See Methods for derivations.

Fig. 6.. Biological implementation of recursive cortical networks (RCN) inference.

(A) RCN factor graph segment for a microcolumn. Since Bio-RCN (B) requires different copies of neurons for forward and backward computations, the factor graph segment is replicated at the bottom left to show the correspondence between cortical layers and computations in the factor graph. The correspondence between RCN computations (A) and Bio-RCN (B) are annotated using circled letters a to i.

Fig. 7.. Cortical microcircuit motifs.

(A) recursive cortical networks (RCN) equations predict that interactions between blob and interblob columns will include different forms of dendritic integration and gating. (B) Detailed microcircuits of contour-contour lateral connections and pooling. The dendrites of the neurons in layer 2/3 encode the compatibility factor (yellow node in the factor graph) between different pools. Columns in a pool also inhibit each other as part of lateral propagation. (C) Ineraction between cortical areas V1 and V2, gated through the thalamus. This pattern of connectivity is a repeating motif between different cortical areas. (D) In the green rectangle: factor graph showing the interaction between cortical columns a, b, and c in V2, with cortical column e in V1, through the factor d. Thalamic relay and thalamic reticular nucleus (TRN) microcircuit predicted by explaining-away computations in RCN and its connections to child and parent cortical columns. A feed-forward pathway originating in V1 layer 5 projects to the relay cells in higher order (HO) thalamus, which are gated by inhibitory TRN cells based on excitatory feedback projections from layer 6 in V2.

Fig. 8.. Subjective contours and neon-color spreading.

(A) Recursive cortical networks (RCN) MAP inference results for stimuli that induce subjective contours in humans. Green, top-down imaginations with bottom-up evidential support. Magenta, contour hallucinations. (B) Layer-wise dynamics of subjective contour formation in Bio-RCN. (C) Stimulus for neon-color spreading and the subjective contour backtrace. (D) Dynamics of color spreading inside the surface, for three different colors.

Fig. 9.. Occlusion versus deletion.

(A) Humans have a harder time perceiving objects with deleted portions compared to the case where the same portions are occluded. Clockwise in each set of four images: (i) Object with occlusion, (ii) the same object with occluded portion deleted, (iii) recursive cortical networks (RCN) MAP inference for occlusion case, (iv), RCN MAP inference for deletion. (B) Recognition accuracy for occlusion versus deletion as a function of the amount of missing evidence. (C) Occlusion versus deletion for MNIST digits. In each row left to right, original digit, occluded digit, MAP inference overlaid on occlusion, digit with occluded portions deleted, MAP inference with deletion. (D) The same as (B) for MNIST digits.

Fig. 10.. Illustration of the two types of message updates.

On the left, update (Eq. 1) (messages from variables to factors), independent of the temperature or the factor definition; on the right, update (Eq. 2) (messages from factors to variables), with the form of the update being specific to each factor and temperature.