Thermalization and criticality on an analogue-digital quantum simulator

Abstract

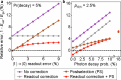
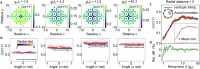
Understanding how interacting particles approach thermal equilibrium is a major challenge of quantum simulators^1,2. Unlocking the full potential of such systems towards this goal requires flexible initial state preparation, precise time evolution and extensive probes for final state characterization. Here we present a quantum simulator comprising 69 superconducting qubits that supports both universal quantum gates and high-fidelity analogue evolution, with performance beyond the reach of classical simulation in cross-entropy benchmarking experiments. This hybrid platform features more versatile measurement capabilities compared with analogue-only simulators, which we leverage here to reveal a coarsening-induced breakdown of Kibble-Zurek scaling predictions³ in the XY model, as well as signatures of the classical Kosterlitz-Thouless phase transition⁴. Moreover, the digital gates enable precise energy control, allowing us to study the effects of the eigenstate thermalization hypothesis^5-7 in targeted parts of the eigenspectrum. We also demonstrate digital preparation of pairwise-entangled dimer states, and image the transport of energy and vorticity during subsequent thermalization in analogue evolution. These results establish the efficacy of superconducting analogue-digital quantum processors for preparing states across many-body spectra and unveiling their thermalization dynamics.

Fig. 1. Analogue–digital simulation with high-precision calibration.

a, Our platform combines analogue evolution with digital gates for extensive state preparation and characterization. b, Schematic of new scalable analogue calibration scheme. Swap (blue) and single-photon (red) spectroscopy is used to extract dressed coupling rates ($\left\{\tilde{g}\right\}$) and qubit frequencies ($\left\{{\tilde{\omega }}_{qi}\right\}$) of two-qubit analogue evolution (U_A), which are converted to bare qubit and coupler frequencies ({ω_qi}, {ω_cj}) through detailed device modelling. The bare frequencies allow for establishing the device Hamiltonian of the full system, which is finally projected to a spin Hamiltonian, H_s.

Fig. 2. Fast thermalization dynamics and beyond-classical capabilities in the high-temperature regime.

a, Schematic representation of the experiment: N_q qubits are initialized in a half-filling state, evolved under a Hamiltonian H_s over time t with four instances of disorder in {ω_i}, and finally measured in the Z-basis. b, Distribution Pr(p) of bitstring probabilities p from experiment (coloured bars) at t = 96 ns ≈ 5.5/g and ideal Porter–Thomas distribution Pr(p) = De^−pD (dashed lines). Inset, convergence of the self-XEB with time. c, Time-dependent XEB fidelity for system sizes up to N_q = 35. Inset, system size dependence of ϵ (error per qubit per evolution time of 1/g) from exponential fits. d, Mixed-state entanglement proxy, ${\mathcal{E}}_{\mathrm{P}}$, obtained in this and previous studies, plotted against the effective system size $N_{\mathrm{q}}^{\mathrm{eff}}$ (with respect to entanglement of a fully chaotic state; Supplementary Information) of the respective platforms. Blue pentagons, Sycamore processor in the digital regime^,; diamonds, Zuchongzhi processor^,; circle, neutral atom analogue simulator; green pentagon, present experiment. $N_{\mathrm{q}}^{\mathrm{eff}}$ is equal to the actual N_q in the digital experiments, whereas analogue platforms are subject to U(1) conservation (this work) or constraints from Rydberg blockade. Inset, ${\mathcal{E}}_{\mathrm{P}}$ as a function of N_q computed from experimental data, including the linear fit used for extrapolation to 69 qubits.

Fig. 3. Critical coarsening in the XY model.

a, Left, experimental schematic of qubit frequencies (blue) and coupling (yellow). Right, phase diagram. Dynamics become diabatic (dashed black) with increased temperature (T) when inverse remaining time (red) exceeds gap (green; Δ ∝ ∣g − g_c∣^νz). QCP and CCP denote the quantum and classical critical phases, respectively. b, The final energy density approaches the ground state value (ε_gs, grey) and Kosterlitz–Thouless transition value (ε_KT, black) as t_r is increased. Red circles and squares indicate single-qubit (SQ) and Bell basis measurements, respectively. Blue, MPS simulation. Purple shading indicates where classical critical behaviour is expected. c, Average correlation, $\overline{G}\left(\mathbf{r}\right)$ (found from averaging (⟨X_iX_j + Y_iY_j⟩ − ⟨X_i⟩⟨X_j⟩ − ⟨Y_i⟩⟨Y_j⟩)/2 over all pairs i, j separated by r) measured at various t_r. d, Decay of radially averaged correlations. Green and purple curves show examples of exponential and power-law fits, respectively, performed up to a distance of 6 to avoid finite-size effects at longer distances. Error bars represent one standard deviation estimated from bootstrapping (N_reps = 5 × 10⁴ repetitions). e, Ratio between r.m.s. errors from power-law and exponential fits (${\mathit{ϵ}}_{\mathrm{pow}}/{\mathit{ϵ}}_{\exp }$) decreases for g_mt_r > 15. f, Power-law exponent, γ, approaches expected value at Kosterlitz–Thouless transition (1/4; black line). g, Vortex density proxy, n_V, decreases to minimum of 2 × 10⁻². h, Correlation length increases with t_r. Both simulation results (blue) and experimental data (red) show substantially more superlinear growth than KZ predictions (dashed black). Diamonds, correlation lengths extracted at expected freezing point (i). i, Correlation length during the ramp, shown with and without rescaling (main and inset, respectively) and two-sided logarithmic axes for ∣τ∣ > τ_KZ. ξ_KZ is found from fitting $\xi \left(\tau ={\tau }_{\mathrm{KZ}}\right)={\xi }_0{\left({\tau }_{\mathrm{KZ}}/t_r\right)}^{-\beta }$ with β = 0.9(1) (difference from β = ν = 0.67 expected to be due to finite-size effects). Dashed coloured lines show the theoretically expected scaling, f(x) = ∣x∣^−ν with ν = 0.67 for x < −1 (purple) and a heuristic f(x) = x^η with η = 1 for x > 1 (teal). The increase in ξ beyond the freezing point (diamond) causes deviation from KZ predictions.

Fig. 4. Tunable thermalized states through initial excitations.

a,b, Energy density (a) and correlation length (b) versus number of initial excitations, n₀, averaged over three randomizations. Error bars smaller than markers (N_reps = 6 × 10³ per data point). c, Energy dependence of ξ, demonstrating collapse when data from sweeps of t_r and n₀ are plotted together. $\log \xi$ is near-linear in ∣ε − ε_KT∣^−0.5 as theoretically expected. Inset, vortex density versus energy density, showing similar collapse. Error estimated from bootstrapping in c and e. d, t_r-dependence of energy density and its fluctuations (width), for various n₀. e, Energy fluctuations versus energy density, showing an absence of collapse becase σ_ε does not thermalize. f, Second Rényi entropy versus subsystem size for various n₀ at t_r = 200 ns ≈ 23/g. Increasing n₀ causes transition from area- to volume-law behaviour, also seen from the extracted contributions (inset, error bars represent one standard deviation across five excitation randomizations and four subsystems).

Fig. 5. Transport and thermalization dynamics with entangled initial states.

a, Dimer states are prepared using digital gates, and their thermalization and transport dynamics are realized with analogue evolution, before finally measuring energy, spin current and vorticity. b, We prepare dimer states with spatially tunable phase, ϕ. Energy gradients between ϕ = 0 (ε > 0) and ϕ = π (ε < 0) drive energy current, whereas ϕ = π/2 gives non-zero spin current and vorticity. c,d, Time evolution of energy density (c) and correlations (d) after dimer preparation demonstrate rapid thermalization. e, Correlations become increasingly long-ranged as the system thermalizes. Dashed line, exponential fit. f,g, Energy density (f) and energy gradients (g) after dimer preparation with ϕ = 0 and π in the left and right halves of the system, respectively, showing energy transport on much longer timescales. Colour and length scales of arrows in g and i are logarithmic. h, Time dependence of average energy density along various vertical cuts (coloured circles) and energy imbalance across x = 5 (black circles), showing very good agreement with diffusion model (dashed lines). Error bars smaller than markers. i,j, Spin current (i) and vorticity (j) for ϕ = π/2, showing rapid thermalization. k, The r.m.s. vorticity shows initial slow dynamics followed by near-exponential decay with rate Γ = 49 MHz = 0.85g (fit shown by dashed line). Error bars in e and k are estimated by bootstrapping (N_reps = 10⁴).

Extended Data Fig. 1. Device characterization.

a,b, Ramsey dephasing ($T_2^{*}$; a) and photon relaxation (T₁; b) times across the qubit grid. c,d, Histogram of Pauli error for combined $\sqrt{\mathrm{iSWAP}}$ and single qubit gates (c) and only single qubit gates (d). Red dashed lines indicate the median values. (CDF: cumulative distribution function). e, Histogram of readout errors.

Extended Data Fig. 2. Schematic of underlying coupling pathways in the device.

In addition to capacitive coupling between neighboring qubits (orange) and couplers (blue), there are also diagonal next-nearest-neighbor couplings. Asymmetry in the underlying structure of the qubits causes a difference in the couplings along the NW-SE and NE-SW diagonals.

Extended Data Fig. 3. Analogue calibration procedure.

a, Overview of calibration steps. We perform three main steps, which together allow for determining the bare frequencies of the qubits and couplers in the idle configuration in which $\tilde{g}=0$ (top row), as well as in the interaction configuration (bottom two rows). For each step, we model a subsystem (third column) to convert the measured dressed frequencies (fourth column) to bare frequencies (fifth column). b, Circuit schematic of swap spectroscopy. c, Top: Measured population difference, ⟨Z₁ − Z₂⟩, as a function of qubit detuning and time. Bottom: Extracted swap rate from Fourier transform vs qubit detuning. The position of the minimum allows for determining $\tilde{g}$ and the difference of the dressed qubit frequencies, ${\tilde{\omega }}_{q1}-{\tilde{\omega }}_{q2}$. d, Circuit schematic of single-photon spectroscopy. e, Fourier transform of the measured ⟨X⟩ + i⟨Y⟩. The average of the peak positions is equal to the average of the dressed qubit frequencies $\left({\tilde{\omega }}_{q1}+{\tilde{\omega }}_{q2}\right)/2$.

Extended Data Fig. 4. Higher order terms in the analogue spin Hamiltonian.

Average coupling coefficient vs nearest-neighbor hopping g for a, n_in_i+1, b, (X_in_i+1X_i+2 + Y_in_i+1Y_i+2)/2, c, (X_iX_i+2 + Y_iY_i+2)/2, and d, n_i(X_i+1X_i+2 + Y_i+1Y_i+2)/2, where qubits i, i + 1, and i + 2 are placed along a connected line. Aside from an offset due to diagonal capacitive coupling, the first three terms scale as g²/η, while the fourth scales as g³η², where η is the anharmonicity. At g = 2π × 10MHz, all higher-order terms are smaller than 1 × 2π MHz. In the three latter terms, there is asymmetry between the three possible configurations displayed in the insets (see text for details). Note that n_i(X_i+1X_i+2 + Y_i+1Y_i+2)/2 does not differ on average from (X_iX_i+1 + Y_iY_i+1)n_i+2/2 in d.

Extended Data Fig. 5. Phase calibration for hybrid analogue-digital experiments.

a, Schematic of phase accumulation and correction throughout hybrid analogue-digital circuit. While we typically prepare initial dimer states, we here consider an initial state $\mid ++⟩$ for the purpose of simplified explanation. Blue and yellow lines show qubit frequency trajectories and coupling profile, respectively, while brown (beige) boxes show the relative alignment of the two spins in the idle (resonance) frame. We apply corrective phases {ϕ_0,i} before the analogue circuit to ensure the correct dimer phase in the resonance frame when the analogue Hamiltonian is turned on. Additional phases {ω_it + ϕ_1,i} are applied after the analogue evolution in order to measure the same phase in the idle frame as was in the resonance frame. b, {ϕ_0,i} are calibrated by preparing triplet states, sweeping the phase difference within each qubit pair, and measuring the population difference after a variable time t. c, Population difference after time t for an applied phase difference ϕ. Since only the dimer phases 0 and π are eigenstates of the analogue Hamiltonian, the correct ϕ_0,i is determined by minimizing the population oscillations. d, {ω_i} are calibrated by performing adiabatic ground state preparation with an initial staggered field and a slow (25/g_m) ramp, and measuring the ⟨XX⟩ correlations a time t after the ramp. e, Top: ⟨XX⟩ after time t when applying no corrective phase after the analogue evolution. Since the low-energy final state is known to have long-range correlations, the observed oscillations can be fit to extract the time-dependent part of the corrective phase after the analogue pulse. Bottom: ⟨XX⟩ after time t when applying the corrective phase found from fitting the oscillations. The near-constant value indicates a successful correction. f, {ϕ_1,i} are calibrated by preparing an initial dimer state, performing the same circuit as in the experiment with corrective pre-analogue phases {ϕ_0,i} and partial post-analogue phases {ω_it}, applying a variable phase ϕ to one qubit in each pair, and measuring the ⟨XX⟩ correlations a time t after the ramp. g, Top: ⟨XX⟩ after time t. Since the state is known to be the triplet state, the correct ϕ₁ is found from maximizing ⟨XX⟩ correlations. Bottom: As a complementary technique, one can prepare the singlet state instead and find the ϕ that minimizes variations in ⟨XX⟩ correlations.

Extended Data Fig. 6. Correction for readout error and photon decay.

Performance of various readout and photon decay correction techniques as a function of a, readout error b, and photon decay probability. The performance is measured as the relative error between the estimated energy (E_est) and the actual ground state energy (E_gs). We find that the combined technique (red) achieves the lowest relative error for a very wide range of parameters.

Extended Data Fig. 7. Comparison of XX- and YY-correlations.

Ramp time dependence of ⟨XX⟩ and ⟨YY⟩ averaged over all nearest-neighbor pairs. The two are found to be very similar, consistent with U(1)-symmetry.

Extended Data Fig. 8. Energy density fluctuations.

a, In addition to {X_i}, {Y_i} and {Z_i}, we measure 8 periodic patterns of XX and YY to find σ_ε. b, ⟨XXYY⟩ has a relatively simple dependence on Euclidean distance (data from measurements shown in a), which can be interpolated to find the remaining terms. c, Energy density fluctuations, σ_ε, displaying good agreement between experiment (red) and simulation (blue); however, at long ramp times, decoherence causes higher fluctuations in the experimental case.

Extended Data Fig. 9. Isotropy of 4-qubit correlators.

a, Dependence of ⟨X_iX_jY_mY_n⟩ on relative position between centers of mass of sites (i, j) and (m, n), showing a substantial degree of isotropy. b, Angular dependence of ⟨X_iX_jY_mY_n⟩, displaying weak π-periodic oscillations that are most pronounced in the regime with longest correlations. c, Comparison of radial interpolation (dashed black) with the actual correlators at distance 5 (colored circles in main) and their average (dashed red in inset). d, Relative difference between radial interpolation and average of actual correlators, as a function of ramp time. The error is on the order of a few percent, and is comparable to the statistical error (error bars estimated from bootstrapping with 48,000 shots at each ramp time).

Extended Data Fig. 10. Correlation fitting.

a,b, Dependence of ⟨X_iX_j + Y_iY_j⟩/2 on Euclidean distance between i and j at various ramp times from experimental data (a) and simulation results (b). In both cases, we observe distortions at longer (≳ 6 sites) distances, attributed to the finite size of our system. c, Root-mean-square fit error for exponential (green) and power-law (violet) fits, as a function of the cut-off distance applied in the fits. Going beyond a distance of 6, we observe a steep increase in the fit error, arising from the effects seen in a and b. d,e, Ramp time dependence of rms error in power-law fits (d) and exponential fits (e) for various fit range cut-offs. Inset of d: Enlarged version of area indicated by red dashed square, showing abrupt increase in error for fit-range cut-offs longer than 7 sites. f,g, Ramp time dependence of rms error ratio (f) and correlation length (g). The drop in the fit error ratio below 1 is observed for all fit range cut-offs shorter or equal to 7 sites (f), and the discrepancy from KZ-scaling (dashed black) persists for all fit range cut-offs (g).