Constant pH Simulation with FMM Electrostatics in GROMACS. (B) GPU Accelerated Hamiltonian Interpolation
- PMID: 39919130
- PMCID: PMC11866765
- DOI: 10.1021/acs.jctc.4c01319
Constant pH Simulation with FMM Electrostatics in GROMACS. (B) GPU Accelerated Hamiltonian Interpolation
Abstract
The structural dynamics of biological macromolecules, such as proteins, DNA/RNA, or their complexes, are strongly influenced by protonation changes of their typically many titratable groups, which explains their pH sensitivity. Conversely, conformational and environmental changes in the biomolecule affect the protonation state of these groups. With a few exceptions, conventional force field-based molecular dynamics (MD) simulations do not account for these effects, nor do they allow for coupling to a pH buffer. The λ-dynamics method implements this coupling and thus allows for MD simulations at constant pH. It uses separate Hamiltonians for the protonated and deprotonated states of each titratable group, with a dynamic λ variable that continuously interpolates between them. However, rigorous implementations of Hamiltonian Interpolation (HI) λ-dynamics are prohibitively slow for typical numbers of sites when used with particle mesh Ewald (PME). To circumvent this problem, it has recently been proposed to interpolate the charges (QI) instead of the Hamiltonians. Here, in the second of two companion papers, we propose a rigorous yet efficient Multipole-Accelerated Hamiltonian Interpolation (MAHI) method to perform λ-dynamics in GROMACS. Starting from a charge-scaled Hamiltonian, precomputed with the Fast Multipole Method (FMM), the correct HI forces are calculated with negligible computational overhead. However, other electrostatic solvers, such as PME, can also be used for the precomputation. We compare Hamiltonian interpolation with charge interpolation and show that HI leads to more frequent transitions between protonation states, resulting in better sampling and accuracy. Our accuracy and performance benchmarks show that introducing, e.g., 512 titratable sites to a one million atom MD system increases runtime by less than 20% compared to a regular FMM-based simulation. We have integrated the scheme into our GPU-accelerated FMM code for the simulation software GROMACS, allowing easy and effortless transitions from standard force field simulations to constant pH simulations.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
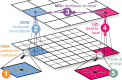

 interactions for Hamiltonian interpolation
(HI). The central magenta box shows the actual simulation volume containing
a two-atomic site (black/green dots), while the surrounding boxes
are periodic images. (A) First, FMM calculates the interactions for
the scaled charges q̃ using multipole expansion
in the yellow areas. (B) Corrections are then computed so that HI
is retrieved for a site with charges QP2P and
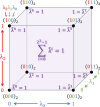
interactions for Hamiltonian interpolation
(HI). The central magenta box shows the actual simulation volume containing
a two-atomic site (black/green dots), while the surrounding boxes
are periodic images. (A) First, FMM calculates the interactions for
the scaled charges q̃ using multipole expansion
in the yellow areas. (B) Corrections are then computed so that HI
is retrieved for a site with charges QP2P and  (green). Here, in contrast to a regular
FMM, all corrections to interactions coming from the first layer around
the central box are computed directly (blue), while corrections from
distant boxes are handled by a lattice operator (yellow).
(green). Here, in contrast to a regular
FMM, all corrections to interactions coming from the first layer around
the central box are computed directly (blue), while corrections from
distant boxes are handled by a lattice operator (yellow).


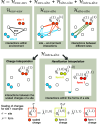
 values in orange, PME in blue.
values in orange, PME in blue.




References
LinkOut - more resources
Full Text Sources
Research Materials
