Subwavelength-scale off-axis optical nanomanipulation within Gaussian-beam traps

Abstract

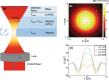
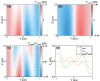
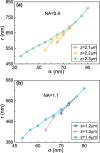
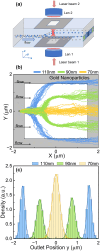
It is generally recognized that there is only a single optical potential-well near the focus in optical traps with a focused Gaussian beam. In this work, we show that this classic Gaussian-beam optical trap has additional optical potential-wells for optical manipulation at the subwavelength scale in the off-focus transverse plane. The additional optical potential-wells are formed by the synergy of both the gradient trapping force and the transverse scattering force, though in previous studies the scattering force usually has adverse effect such as reducing trapping stability. These potential-wells work for not only the metallic particles, but also the high refractive-index dielectric particles. By engineering the contribution of the gradient force and scattering force through the particle size, the particle material and the position of the manipulation transverse plane, the force field and trapping potential-well can be tailored to trap/manipulate nanoparticles at different off-axis distance at the subwavelength scale. Our work provides new insight into optical tweezers and promises applications in optical nanomanipulation, nanoparticle sorting/separation, particle patterning and micro-fabrication on substrates.

Keywords: multiple potential-wells; off-axis trapping; optical manipulation; particle sorting; transverse scattering force.

Figure 1:

Off-axis optical manipulation at off-focus location utilizing the transverse scattering force. (a) Illustration of the setup for off-focus optical manipulation in a focused Gaussian beam. (b) Field intensity ${\left|\mathbf{E}\right|}^2$ and force field F for a gold nanoparticle with radius a = 80 nm on the xy-plane when z = 2.3 μm. The gray dashed line denotes the locations where the value of the force in the radial direction is equal to zero. (c) Potential U _y along the y-direction for the gold nanoparticle when z = 2.1 μm, 2.2 μm, 2.3 μm, and 2.4 μm. The beam is an x-direction linearly polarized Gaussian beam propagating in the z-direction in water; NA = 0.9; light power P = 100 mW and vacuum wavelength λ ₀ = 1,064 nm.

Figure 2:

Field distribution of a focused Gaussian beam at the off-focus location and the off-axis optical trapping in water. (a) Intensity field ${\left|\mathbf{E}\right|}^2$ on the yz-plane. (b) Electric field distribution along y-axis when z = 2.1, 2.2, 2.3, and 2.4 μm. (c) The total optical force F _y along y-axis for a gold nanoparticle with radius a = 80 nm. Other parameters are the same as those in Figure 1.

Figure 3:

Numerically calculated forces and potential-wells of a gold nanoparticle with radius a = 80 nm for off-axis trapping in a focused Gaussian beam. (a) Force F _y on the yz-plane. The black dashed curve denotes the F _y = 0 positions. (b) Potentials U _y with unit of k _B T (T = 25 °C) on the yz-plane within the range of 1.5 μm < z < 3 μm. The area circled by the dark-blue dashed rectangular box will be magnified in figure (c). (c) Potentials U _y on the yz-plane for the gold nanoparticle within the range of 2 μm < z < 2.3 μm. The black dashed lines mark the locations of the local minima of the potential U _y . Other parameters are the same as those in Figure 1.

Figure 4:

Numerically calculated forces of a gold nanoparticle with radius a = 80 nm for off-axis trapping in a focused Gaussian beam. (a) Force F _y,grad on the yz-plane. (b) Force F _y,scat on the yz-plane. (c) Force F _y,grad + F _y,scat on the yz-plane. (d) F _y along y-axis when z = 2.3 μm on the yz-plane. The black dashed curves in subfigures (a–c) mark the positions where the forces are zeros. Other parameters are the same as those in Figure 1.

Figure 5:

Numerically calculated off-axis trapping positions within a focused Gaussian beam with different particle radii and different numerical apertures of the objective lenses. (a) Off-axis trapping positions of gold nanoparticles with different radii for NA = 0.9 at z = 2.1, 2.2, and 2.3 μm. (b) Off-axis trapping positions with different particle radii for NA = 1.1 at z = 1.2, 1.3, and 1.4 μm. Other parameters are the same as those in Figure 1.

Figure 6:

Demonstration of gold nanoparticle separation/sorting. (a) Illustration of the setup for particle sorting. (b) Simulated trajectories of gold nanoparticles with different radii a in the xy-plane when z = 2.2 μm. The light field is limited in the white square of side length 3 μm by masks. The velocity of water flow is 500 μm/s. (c) Particle distributions of different gold nanoparticles at the outlet (x = 2.0 μm). Other parameters are the same as those in Figure 1.

Figure 7:

Numerically calculated off-axis trapping and sorting of dielectric particles with different refractive index in Gaussian beams. (a) Off-axis trapping positions of 120 nm-radius dielectric particles with different refractive indices for NA = 0.9 at z = 2.1, 2.2, and 2.3 μm (b) simulated trajectories of silicon nanoparticles with different radii a in the xy-plane when z = 2.2 μm. The light field is limited with the 1.5 μm × 3 μm light window denoted by the white area. The velocity of water flow is 150 μm/s. Other parameters are the same as those in Figure 1.