Statistical method accounts for microscopic electric field distortions around neurons when simulating activation thresholds
- PMID: 39938863
- PMCID: PMC12009170
- DOI: 10.1016/j.brs.2025.02.007
Statistical method accounts for microscopic electric field distortions around neurons when simulating activation thresholds
Abstract
Introduction: Notwithstanding advances in computational models of neuromodulation, there are mismatches between simulated and experimental activation thresholds. Transcranial Magnetic Stimulation (TMS) of the primary motor cortex generates motor evoked potentials (MEPs). At the threshold of MEP generation, whole-head models predict macroscopic (at millimeter scale) electric fields (50-70 V/m) which are considerably below conventionally simulated cortical neuron thresholds (175-350 V/m).
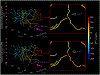
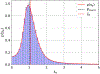
Methods: We hypothesize that this apparent contradiction is in part a consequence of electrical field warping by brain microstructure. Classical neuronal models ignore the physical presence of neighboring neurons and microstructure and assume that the macroscopic field directly acts on the neurons. In previous work, we performed advanced numerical calculations considering realistic microscopic compartments (e.g., cells, blood vessels), resulting in locally inhomogeneous (micrometer scale) electric field and altered neuronal activation thresholds. Here we combine detailed neural threshold simulations under homogeneous field assumptions with microscopic field calculations, leveraging a novel statistical approach.
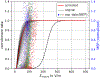
Results: We show that, provided brain-region specific microstructure metrics, a single statistically derived scaling factor between microscopic and macroscopic electric fields can be applied in predicting neuronal thresholds. For the cortical sample considered, the statistical method matches TMS experimental thresholds.
Conclusions: Our approach can be broadly applied to neuromodulation models, where fully coupled microstructure scale simulations may not be computationally tractable.
Keywords: Biophysical modeling; Brain stimulation; Multiscale brain modeling; TMS.
Copyright © 2025 The Authors. Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of competing interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures


Update of
-
Statistical method accounts for microscopic electric field distortions around neurons when simulating activation thresholds.bioRxiv [Preprint]. 2025 Feb 5:2024.10.25.619982. doi: 10.1101/2024.10.25.619982. bioRxiv. 2025. Update in: Brain Stimul. 2025 Mar-Apr;18(2):280-286. doi: 10.1016/j.brs.2025.02.007. PMID: 39484517 Free PMC article. Updated. Preprint.
References
-
- Balanis Constantine A., Advanced Engineering Electromagnetics, Dec, 8, 2023, Print ISBN:9781394180011 |Online ISBN:9781394180042 |DOI:10.1002/9781394180042. - DOI
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

