Galloping Bubbles

Abstract

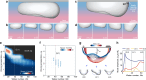
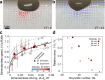
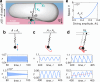
Despite centuries of investigation, bubbles continue to unveil intriguing dynamics relevant to a multitude of practical applications, including industrial, biological, geophysical, and medical settings. Here we introduce bubbles that spontaneously start to 'gallop' along horizontal surfaces inside a vertically-vibrated fluid chamber, self-propelled by a resonant interaction between their shape oscillation modes. These active bubbles exhibit distinct trajectory regimes, including rectilinear, orbital, and run-and-tumble motions, which can be tuned dynamically via the external forcing. Through periodic body deformations, galloping bubbles swim leveraging inertial forces rather than vortex shedding, enabling them to maneuver even when viscous traction is not viable. The galloping symmetry breaking provides a robust self-propulsion mechanism, arising in bubbles whether separated from the wall by a liquid film or directly attached to it, and is captured by a minimal oscillator model, highlighting its universality. Through proof-of-concept demonstrations, we showcase the technological potential of the galloping locomotion for applications involving bubble generation and removal, transport and sorting, navigating complex fluid networks, and surface cleaning. The rich dynamics of galloping bubbles suggest exciting opportunities in heat transfer, microfluidic transport, probing and cleaning, bubble-based computing, soft robotics, and active matter.

Fig. 1. Galloping bubbles.

a Time sequence illustrating a self-propelling bubble under the upper boundary of a vertically vibrating fluid chamber (Supplementary Movie 1), exhibiting shape oscillations reminiscent of galloping motion. The inset includes a schematic of the setup, and T  =  2π/ω is the oscillation period. The bubbles were backlit through a gradient filter to enhance their aesthetic appeal. Different bubble sizes and vibrational forcings produce diverse domain exploration modes, observed from the top view (b–d), Supplementary Movie 2). A bubble may gallop in (b) steady rectilinear motion in an infinite bath, with its trajectory becoming circular here due to the chamber’s boundary (dashed line, see Methods, Experiments). Time progression is indicated by the green arrow, with increasing opacity indicating later times, and the image sequence intervals are 20 T. Depending on the bubble volume, increasing the forcing amplitude A may cause the bubble’s trajectory to curve, leading to orbital states (c), which can develop anywhere within the chamber, or become jagged with random sharp turns (d) reminiscent of ‘run-and-tumble’ motion^,. e A phase map at f = 40 Hz illustrates the dependence of the bubble’s dynamics on the driving acceleration and bubble volume, which also includes detachment from the wall for smaller bubbles and breakup for large amplitudes.

Fig. 2. Hemispherical galloping bubbles and their spectrum.

a, b Direct numerical simulations capture the galloping dynamics (Supplementary Movie 3). As in the experiments, where a thin fluid layer separates the bubble from the boundary, no contact line is formed at the top wall in our model. c, d Simulations demonstrate that the same galloping instability arises for sessile bubbles with a freely moving contact line and 90^∘ contact angle. e A quantitative comparison of bubble speed between experiments (background) and simulations of full bubbles (marker colors and sizes reflect the galloping speed) across a range of normalized driving acceleration, $\gamma$/g, and dimensionless frequency given by the Weber number, We. Galloping motion is observed near We  =  40, corresponding to the natural frequency of the (3,1) vibration mode (indicated by the vertical dashed line). f Hemispherical bubbles exhibit galloping dynamics in the same region of the phase map, and (g) their shape oscillations, which lead to a net displacement Δx per period, are primarily composed of the (k,l)  =  (2,0), (3,1), and (4,0) spherical harmonics, Y_kl(θ,φ). h Mode dominance vs We number for fixed driving A/R  =  0.08 characterized via the L₂ norm of the instantaneous amplitude ∥a_kl(t)/A∥₂. The emergence of the (3,1) harmonic coincides with the onset of galloping.

Fig. 3. Propulsion mechanism.

a, b Experimental visualization of flow fields around a galloping bubble reveals the interface (a) pushing ambient fluid towards the bubble’s back when moving downwards, and (b) drawing fluid from its front when moving upwards (Supplementary Movie 4). c Rectilinear galloping bubbles obey a power scaling law for the dimensionless galloping speed V/ωR in terms of the dimensionless driving (A−A_G)/R and Weber number We, which collapses the simulated hemispherical bubbles with a power α  = 0.29. d The relative deviation between the galloping speed in simulated hemispherical bubbles, V_s, and that expected from inviscid theory, V_t, decreases with the Reynolds number, indicating that galloping bubbles leverage inertial forces for propulsion.

Fig. 4. Oscillator model.

a A weakly deformable pendulum with spring constant k, point mass M, and equilibrium length L, subject to vertical oscillations exhibits a symmetry breaking analogous to that of galloping bubbles. b–d The pendulum’s trajectory (red) is depicted through the instantaneous x₀ − y₀ coordinates relative to the pivot. b At low forcing amplitude, the motion is purely vertical. c Above a critical threshold, A > A_G, the mass acquires angular momentum due to the coupling between vertical base oscillations and spontaneously emerging lateral oscillations. d If the pivot is allowed to slide, the mass motion gives rise to horizontal translation, where (e) the steady propulsion speed V is proportional to A − A_G. The model parameters are κ = 0.05, p = 0.3, ζ = 0.02, δ = 1.1 and (b) ε = 0.2, (c) ε = 0.4, and (d) ε = 0.6, ζ_p = 0.2, ξ = 100 (Methods, Theory).

Fig. 5. Applications of galloping bubbles.

a Bubble evacuation: the galloping instability enables the removal of bubbles from a nucleation point, which hinder heat transfer in boiling. b Size selection: keeping the injection flow rate constant, bubble generation with tunable size becomes possible through the driving frequency, which determines when the bubbles start to gallop away from the nozzle. c Size-dependent sorting: owing to their affinity to follow lateral boundaries, bubbles of various volumes are autonomously directed into collectors of decreasing sizes, facilitating their sorting. d Navigation through complex networks: galloping bubbles have an ability to navigate intricate flow networks and solve mazes. The colored lines and arrows represent paths taken by different bubbles from the entrance until they reach the exit (red: f  =  50 Hz at A = 0.39 mm, white: 45 Hz at 0.37 mm, and blue: 40 Hz at 0.54 mm). e Surface cleaning: particles covering a surface may be removed through the flows generated by bubbles exploring the domain randomly (See Supplementary Movie 5).