Negative refraction of light in an atomic medium

Abstract

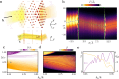
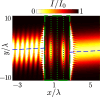
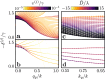
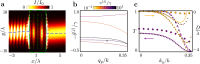
The quest to manipulate light propagation in ways not possible with natural media has driven the development of artificially structured metamaterials. One of the most striking effects is negative refraction, where the light beam deflects away from the boundary normal. However, due to material characteristics, the applications of this phenomenon, such as lensing that surpasses the diffraction limit, have been constrained. Here, we demonstrate negative refraction of light in an atomic medium without the use of artificial metamaterials, employing essentially exact simulations of light propagation. High transmission negative refraction is achieved in atomic arrays for different level structures and lattice constants, within the scope of currently realised experimental systems. We introduce an intuitive description of negative refraction based on collective excitation bands, whose transverse group velocities are antiparallel to the excitation quasi-momenta. We also illustrate how this phenomenon is robust to lattice imperfections and can be significantly enhanced through subradiance.

Fig. 1. Negative refraction and transmission of light through an atomic medium.

a Schematic shows light transmission through a cubic atom array, stacked in infinite planar lattices along the x-axis, with the incident beam propagating towards x = ∞. The dominant wavevector k lies in the xy plane at angle $\theta =\arcsin \left(k_y/k\right)$ to the lattice normal, tilting in the y direction. The transmitted beam undergoes lateral displacement D along the y-axis. b Negative refraction of a beam incident with θ = 0.2 × π and laser detuning Δ/γ = 0.73 from the atomic resonance, in units of single-atom linewidth γ, through a 25-layer atomic lattice for the $J=0\to J^{\prime }=1$ transition. This is manifested in the normalised light intensity profile I/I₀ (outside the medium) and atomic polarisation density $\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }^2/\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }_{\max }^2$ (within the lattice delimited by the dashed green box) at plane z = 0, scaled by resonance wavelength λ, where $I_0=2{ϵ}_{0}c{\max }_{\mathbf{r}}\mid {\mathcal{E}}^{+}\left(\mathbf{r}\right){\mid }^2$ represents the maximum incident intensity. For visualisation, $\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }^2/\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }_{\max }^2$ for point-like atoms is smoothed by convolution with a Gaussian of the root-mean-square widths σ_x = 0.25a and σ_y = 0.5a. The blue dashed lines trace the peak light intensity, while the connecting green line marks the effective trajectory in the medium. c D/λ and d power transmission T as a function of Δ/γ and k_y/k across the transmission band. Green stars denote the parameters taken in b for the incident beam. e Variation of T and effective group refractive index $n_{\mathrm{eff}}^{\prime }$ with k_y/k, for the same laser detuning as in (b).

Fig. 2. Negative refraction in a 5-layer lattice of two-level atoms with Rb lattice spacing.

Transmission of light through a cubic array of atoms, formed by five stacked infinite planar lattices. Each atom, denoted by a green dot, exhibits an isolated σ⁺-polarised two-level transition, with the quantisation axis along z, and a lattice constant a = 0.68λ, corresponding to Mott insulator-state experiments of Rb atoms^,. Negative refraction is demonstrated by normalised light intensity I/I₀ outside the medium at the plane z = 0, where $I_0=2{ϵ}_{0}c{\max }_{\mathbf{r}}\mid {\mathcal{E}}^{+}\left(\mathbf{r}\right){\mid }^2$ represents the maximum incident field intensity. Within the lattice, delimited by the dashed green box, the atomic polarisation density $\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }^2/\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }_{\max }^2$ is visualised and smoothed using convolution with a Gaussian of root-mean-square widths σ_x = 0.25, σ_y = 0.5. The light beam, incident in the xy plane at angle $\theta =\arcsin \left(0.2\right)$ to the lattice normal and with a detuning Δ = −0.1γ from the atomic resonance, shows a lateral displacement along the y-axis of approximately −λ and power transmission T ≃0.95.

Fig. 3. Collective resonance excitation band structure and beam displacement for the J=0→J′=1 transition.

a 25-layer b 5-layer collective line shifts δ^(j)(q_y, q_z = 0), in units of the single-atom linewidth γ, for atomic Bloch wave resonances across bands indexed by j, as a function of in-plane quasimomentum q_y, indicative of the incident light’s tilting angle. The lattice spacing a = 0.45λ, in units of resonance wavelength λ. The colour coding indicates the collective resonance linewidth (see Methods), υ^(j)(q_y, q_z = 0), on a logarithmic scale, normalised to γ. c 25-layer d 5-layer exact (scatter points) lateral displacement D(k_∥, −δ^(j)(k_y, 0)), in units of λ, compared with approximate (solid lines) lateral beam displacement $\tilde{D}\left({\mathbf{k}}_{\parallel },-{\delta }^{\left(j\right)}\left(k_y,0\right)\right)=v_{g,y}^{\left(j\right)}/{\upsilon }^{\left(j\right)}\left(k_y,0\right)$, derived from the group velocity $v_{g,y}^{\left(j\right)}=-\partial {\delta }^{\left(j\right)}\left(k_y,0\right)/\partial k_y$ along the y-axis for laser detuning Δ = −δ^(j)(k_y, 0) resonant with band j, considering the incident light’s wavevector y-component k_y.

Fig. 4. Microscopic origin of negative refraction and emergence of macroscopic optical bulk response.

a Schematic illustrates the microscopic mechanism of negative refraction. An atomic polarisation wavepacket, excited by the incident beam, propagates along the y-axis over its lifetime t = 1/υ, where υ = υ^(j)(q_y, q_z = 0) is the collective linewidth, accumulating a transverse displacement of D ≃v_g,y × 1/υ. The transverse group velocity component v_g,y = −∂δ^(j)(q_y, q_z = 0)/∂q_y is derived from the collective line shifts δ^(j)(q_y, q_z = 0) for phase-matched quasimomenta q_y in resonant band j. Green and grey wavepackets illustrate cases of negative and positive displacement, respectively. For b N_x = 25, c N_x = 50, and d N_x = 100 infinite layers, collective line shifts, in units of the single-atom linewidth γ, are presented for the lattice spacing a = 0.45λ, where λ is the resonance wavelength. The in-plane quasimomentum, indicative of the incident light’s tilting angle, is varied. The collective resonance linewidth is normalised to γ/(N_x − 1) on a colour-coded logarithmic scale. This choice highlights the linear dependence of the wavepacket lifetime, and displacement D, on sample thickness a(N_x − 1), as alluded to in (a). Anomalous bright dots correspond to resonances due to array edges in the x-direction.

Fig. 5. Effects of finite lattice size and imperfections on negative refraction.

a Negative refraction of light through a 5 × 25 × 25 atomic array, denoted by green dots, with spacing a = 0.68λ, resonance wavelength λ, and an isolated σ⁺-polarised two-level transition. The light is incident in the xy plane at angle $\theta =\arcsin \left(0.2\right)$ to the lattice normal, with laser detuning Δ = −0.1γ from the atomic resonance, scaled by the single-atom linewidth γ. The image shows the normalised light intensity profile I/I₀ (outside the medium) and atomic polarisation density $\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }^2/\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }_{\max }^2$ (within the lattice delimited by the dashed green box) at plane z = 0, scaled by λ, where $I_0=2{ϵ}_{0}c{\max }_{\mathbf{r}}\mid {\mathcal{E}}^{+}\left(\mathbf{r}\right){\mid }^2$ represents the maximum incident intensity. $\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }^2/\mid ⟨\widehat{\mathbf{P}}{}^{+}⟩{\mid }_{\max }^2$ for point-like atoms is smoothed by convolution with a Gaussian of the root-mean-square widths σ_x = 0.25a and σ_y = 0.5a. The blue dashed lines trace the peak light intensity. b Collective line shifts δ^(j)(q_y, q_z = 0), in units of γ, for atomic Bloch wave resonances across bands indexed by j in the corresponding lattice with infinite in-plane layers. The in-plane quasimomentum q_y, indicative of the incident light’s tilting angle, is varied. The colour coding represents the collective resonance linewidth (see Methods), υ^(j)(q_y, q_z = 0), on a logarithmic scale, normalised to γ. In contrast with Fig. 3b, the larger lattice spacing gives rise to diffraction of phase-matched beams once q_y ≳0.48k, so we restrict the quasimomentum q_y ≲0.35k to lie well within this range. The green star denotes the dominantly excited resonance with linewidth  ≃0.05γ in (a). c Power transmission T and lateral displacement D from the centre of the layer at the exit (not the displacement of the incident beam), in units of λ, as a function of the incident light’s wavevector y-component k_y. Perfect lattice with infinite layers (dashed lines) and finite-size layers (dotted lines); atomic position fluctuations with 1/e density width 0.074a about each site, obtained from stochastic simulations (diamonds); phenomenological model with corresponding imperfection parameter ζ_f = 0.975 with infinite layers (solid lines) and finite-size layers (stars).