Quantum geometry in condensed matter

Abstract

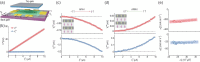
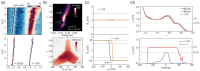
One of the most celebrated accomplishments of modern physics is the description of fundamental principles of nature in the language of geometry. As the motion of celestial bodies is governed by the geometry of spacetime, the motion of electrons in condensed matter can be characterized by the geometry of the Hilbert space of their wave functions. Such quantum geometry, comprising Berry curvature and the quantum metric, can thus exert profound influences on various properties of materials. The dipoles of both Berry curvature and the quantum metric produce nonlinear transport. The quantum metric plays an important role in flat-band superconductors by enhancing the transition temperature. The uniformly distributed momentum-space quantum geometry stabilizes the fractional Chern insulators and results in the fractional quantum anomalous Hall effect. Here we review in detail quantum geometry in condensed matter, paying close attention to its effects on nonlinear transport, superconductivity and topological properties. Possible future research directions in this field are also envisaged.

Keywords: Berry curvature; flat-band superconductor; fractional Chern insulator; nonlinear transport; quantum geometry; quantum metric.

Figure 1.

(a) The demonstration of distance between two adjacent quantum states and . (b) Various types of nonlinear transport associated with quantum geometry. Nonlinear longitudinal conductivity emerges from band geometry and is observable in the antiferromagnetic topological insulator MnBiTe [27]. On the other hand, the nonlinear Hall effect can be categorized into two groups: (i) the electric nonlinear Hall effect and (ii) the magneto-nonlinear Hall effect. The former may arise from the Berry curvature dipole (e.g. in WTe [15,16], MoTe [18,19], WSe [17], CdAs [20], CeBiPd [22] and TaIrTe [21]) or the quantum metric dipole (e.g. in MnBiTe [26,27]), while the latter has been observed in the kagome magnet FeSn [28].

Figure 2.

Electric nonlinear Hall effect in WTe. (a) Schematic plot of a dual-gated bilayer WTe device encapsulated in hexagonal boron nitride electrodes. (b) Nonlinear Hall (red) and longitudinal (green, purple) voltages versus the driving current . Panels (a) and (b) are adapted from [15]. (c) Optical image of a Hall bar device of few-layer WTe. (d) Nonlinear Hall voltages. The driving current flows from the source (S) to the drain (D) and voltages are measured between electrodes A and B. Panels (c) and (d) are adapted from [16].

Figure 3.

Electric nonlinear Hall effect and longitudinal conductivity. (a) Schematic plot of a six-end Hall bar device of four septuple-layer MnBiTe (green) with a top gate (grey) and a back gate (purple). An ac driving current is applied along the x direction, while linear/nonlinear voltages are measured along the x and y directions using the standard lock-in technique. (b) Linear longitudinal (red) and Hall (blue) voltages. (c),(d) Nonlinear longitudinal (red) and Hall (blue) voltages for the AFM-I and AFM-II phases of MnBiTe. Insets illustrate the magnetization of each septuple layer in the AFM-I and AFM-II phases. (e) Scaling of the nonlinear Hall (red) and longitudinal (blue) conductivities with respect to the square of the linear longitudinal conductivity. The dashed lines are the linear fits according to Equation (20). All panels are adapted from [27].

Figure 4.

(a) Schematic atomic structure of FeSn with gold (blue) balls representing iron (stannum) atoms. (b) Angle-resolved Hall resistivity for a magnetic field in the z-x plane. (c) Angle-resolved Hall resistivity for a magnetic field in the y-z plane. Inset: in-plane Hall resistivity occurs with a y-direction magnetic field. (d) Magnetic field dependence of Hall resistivity at different temperatures. (e) The component of the anomalous orbital polarizability projected onto the first-principles band structure. (f) Distribution of the anomalous orbital polarizability dipole on the Fermi surface, where a pair of Weyl points serve as the hot spots. All panels are adapted from [28].

Figure 5.

Schematic plot of Wannier function overlap. (a) A single flat band formed by well-separated Wannier functions in the absence of interactions. (b) A single flat band robust against interaction that does not create sizable Wannier function overlap. (c) A flat band in a multi-band system formed by the destructive interference of Wannier functions. (d) Interaction interrupts the destructive interference and causes a supercurrent. Reproduced with changes from [70].

Figure 6.

(a) Lattice structure of twisted bilayer graphene. (b) Band structure of twisted bilayer graphene plotted along the high-symmetry path. Inset: the Moiré Brillouin zone. The nearly flat bands are highlighted with colors. (c) Superfluid weight versus filling at and . (d) Superfluid weight versus the superconductor gap. Thick blue: full superfluid weight. Red: superfluid weight calculated with eight lowest-energy bands (four dispersive, four nearly flat). Yellow: superfluid weight calculated with four nearly flat bands. Blue: conventional superfluid weight. (e) Longitudinal resistance versus gate voltage of twisted bilayer graphene. Shade marks the filling where superconductivity occurs. (f) Resistivity in the -T plane shows a superconducting dome (dark blue). (g) Resistivity in the -B plane shows a superconducting dome (dark blue). (h) Differential resistivity in the -J plane shows a superconducting dome (dark blue). The dome boundary (red dashed curve) marks the critical supercurrent. (i) Superfluid weight, calculated with critical supercurrent (red) via Equation (37), is well fitted by including the geometric contribution (green) and dominates over the conventional contribution approximated by (black). Panels (a), (b) and (d) are adapted from [36]. Panel (c) is adapted from [35]. Panels (e)–(i) are adapted from [37].

Figure 7.

(a) Local inverse compressibility in the -B plane. Here is the filling per Moiré unit cell and B is the applied magnetic field. (b) The line trajectories in the inverse compressibility measurement are classified as Chern insulators/integer quantum Hall states (black), correlated insulators (green), charge density waves (cyan), translational symmetry-broken Chern insulators (yellow) and fractional Chern insulators (red). (c) Enlarged view of panel (b) in the low-field regime. (d) Enlarged view of panel (b) in the high-field regime. (e) Standard deviation of Berry curvature as a function of the magnetic field for a realistic magic-angle twisted bilayer graphene with. Fractional Chern insulating (CDW) phase is observed at the high-field (low-field) regime. The onset of the fractional Chern insulating phase is approximately located at and . (f) Standard deviation of Berry curvature as a function of the ratio of twisted bilayer graphene at zero applied magnetic field. The onset of the fractional Chern insulating phase is approximately at the ratio . (g) The phase diagram of twisted bilayer graphene in the - plane. The CDW is located in the lower right corner. The transition to fractional Chern insulators occurs in the regime . All panels are adapted from [48].

Figure 8.

(a) Incompressibility measurement of twisted bilayer MoTe. Integer (blue) and fractional (black) Chern insulators are respectively observed for hole fillings and . Adapted from [52]. (b) Trion photoluminescence exhibits blueshifts at and , respectively indicating integer and fractional Chern insulating states, which are also observable in the reflective magnetic circular dichroism measurement. Adapted from [51]. (c) Longitudinal and Hall resistances versus the magnetic field in twisted bilayer MoTe. Plateaus are observed at , corresponding to fractional filling . Adapted from [53]. (d) Hall conductance versus filling/displacement in twisted bilayer MoTe. Fractional Hall conductance is the smoking-gun evidence of fractional Chern insulators. Adapted from [54].