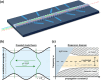
General design flow for waveguide Bragg gratings

Abstract

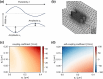
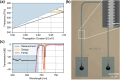
Bragg gratings are crucial components in passive photonic signal processing, with wide-ranging applications including biosensing, pulse compression, photonic computing, and addressing. However, the design of integrated waveguide Bragg gratings (WBGs) for arbitrary wavelengths presents significant challenges, especially when dealing with highly asymmetric layer stacks and large refractive index contrasts. Convenient approximations used for fiber Bragg gratings generally break down in these cases, resulting in nontrivial design challenges. In this work, we introduce a general simulation and design framework for WBGs, which combines coupled mode theory with three-dimensional finite-element method eigenfrequency computations. This approach allows for precise design and optimization of WBGs across a broad range of device layer stacks. The design flow is applicable to further layer stacks across nearly all wavelengths of interest, given that the coupling between the forward and backward propagating mode is dominant.

Keywords: integrated signal processing; photonic longpass filter; waveguide Bragg gratings.

Figure 1:

Waves in periodic structures. (a) The periodic modulation of the waveguide structure enables molding the flow of light. The spectral response depends on the frequency and effective index of the electromagnetic waves and can lead to scattering to the cladding or substrate, back reflection in the waveguide or unaffected transmission through the waveguide. (b) Coupled mode theory offers an effective way to simulate and design the propagation properties of a waveguide Bragg grating by expanding the modes of the structure in terms of eigenmodes of the unperturbed waveguide. It is often sufficient to only consider coupling between the forward and backward propagating fundamental mode. (c) The dispersion diagram for a uniform, infinite long periodic structure offer additional insight in the propagation properties. The modulation splits the fundamental mode into a dielectric band and air band, separated by a photonic band gap. Furthermore, the light line indicates the scattering into the substrate or cladding.

Figure 2:

Simulation and design framework. (a) We design the grating cell as a sine modulation of the waveguide width, where the modulation from outside to inside and vice versa are tuned independently via the amplitudes a₁ and a₂. The waveguide width is set to the default width of the photonic circuit, and the periodicity determines the general spectral response. (b) For a given periodicity and width, we compute the eigenfrequency of the grating cell for various values of a₁ and a₂ at the edge of the Brillouin zone β = π/Λ. As the simulation domain only contains a single grating cell, complete finite element method simulations with a fine mesh can be performed in reasonable time. (c, d) Based on the FEM simulations, we can compute the width and position of the bandgap and hence the coupling coefficient for the coupled mode theory approximation.

Figure 3:

Apodized waveguide Bragg gratings. (a) In order to fabricate a 5 nm notch filter with suppressed sidelobes, we apodize the coupling coefficient with a Gaussian window. The self-coupling coefficient needs to remain constant, in this case zero, to avoid asymmetric reflection spectra. (b) We use the FEM simulations to map the coupling coefficients to the physical design parameters of the grating cell. (c) We fabricate air-clad waveguides and filters on the 330 nm silicon platform. We place two identical WBGs in a Mach–Zehnder Interferometer-like structure to separate the reflected light from the input light. (d) We measure the transmission spectrum for three different gratings with a periodicity of 500 nm, 506 nm, and 511 nm, respectively. We can use the same FEM simulation, performed for a periodicity of 500 nm, for all designs as the coupling coefficients are invariant for small variations of the periodicity.

Figure 4:

Broadband visible filter. (a) The dispersion diagram shows the dielectric and air band of the fundamental mode separated by the band gap (yellow-shaded region), the dielectric band of the first-order mode and the light cone (blue-shaded region). The periodic modulation of the waveguide structure leads to significant coupling to substrate modes if no guided mode exists for the given frequency. (b) We fabricate a Bragg grating with 2000 elements and a periodicity of 229 nm on the 100 nm TaO platform that implements a longpass filter. The SEM image shows a single grating cell of the structure. We achieve broadband coupling to the photonic circuit by deploying 3d-printed total internal reflection couplers. (c) We measure the transmission spectrum of the low-cut filter normalized to the back loop reference transmission. For small wavelengths, the coupling to unbound modes decreases the transmission by about −25 dB. The loss within the dielectric band is as low as −0.4 ± 0.1 dB.