Scaling in Biological Systems: A Molecular-Ensemble Duality

Abstract

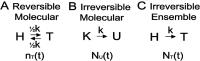
We have observed in muscle the statistical mechanics of irreversible chemical thermodynamics, revealing the solution to multiple seemingly unrelated paradoxes in science. Analogous to Boltzmann's H theorem, we observe that chemical reaction energy landscapes (ensemble entropic wells) irreversibly evolve over time, pulling reversible chemical reactions forward in time. Loschmidt's paradox assumes that reversible molecular reactions scale up to irreversible changes in an ensemble, and many mathematical constructs have been created to satisfy this assumption (Boltzmann's H-function, chemical activities, the kinetics theory of gases, molecular mechanisms of biological function, etc.). However, using a simple statistical argument, here we show that the irreversible time evolutions of molecular and ensemble states are described by two different non-scalable entropies, creating a molecular-ensemble duality in any system on any scale. This inverts common understandings of mechanistic agency and the arrow of time and disproves all molecular mechanisms of irreversible ensemble processes.

Fig. 1.. Three kinetic schemes for coins.

(A) When individual coins are tossed at a rate, k, they reversibly transition between heads, H, and tails, T, at a rate of ½k in each direction. The number of coins in state T, n_T(t), is observed to reversibly change with time as dn_T(t)/dt = – ½n_T(t)·k + ½n_H(t)·k. (B) When coins are tossed at a rate, k, they irreversibly transition from a known, K, to an unknown, U, state, at a rate, k. The number of known coins, N_K(t), irreversibly changes with time as dN_K/dt = −N_K·k. (C) When an ensemble of coins is tossed at a rate, k, they irreversibly transition from heads, H, to tails, T. The number of coins in state T, n_T(t), follows the predictable statistics of the irreversible time course of the microstate, N_T(t), which we show changes with time as d(N_H – N_T)/dt = (N_H – N_T)·k.

Fig. 2.. Molecular and ensemble kinetics and entropy.

(A) The stochastic tossing of ten coins at a rate, k, are simulated (Monte Carlo) with a random number that gives each coin a 10% chance of flipping every 0.1 seconds. A second random number gives a flipped coin a 50% chance of being either heads, H, or tails, T. Transitions between H (lower) and T (upper) are shown (black lines) over time along with coin tosses indicated by red circles. (B) An increase in N_T by ½ at each time-to-first-flip (the first red circle in each trajectory in panel A) is plotted (red circles) along with the sum of all ten trajectories (black squares). The line is N_H = ½N – ½N·exp(−kt). (C) Sequential changes in molecular states from (A) are illustrated. (D) The ensemble states are pulled toward N_T = 5 with time. (E) Molecular entropy, N_u·ln(2), calculated from the molecular transient in (B) is plotted. (F) Ensemble entropy, ln[N!/(N_H!N_T!)], calculated from the ensemble transient in (B) is plotted. (G) The N_U-dependence of molecular entropy, N_u·ln(2), is plotted. (H) The N_T-dependence of ensemble entropy, ln[N!/(N_H!N_T!)], is plotted.