Volumetric imaging of the 3D orientation of cellular structures with a polarized fluorescence light-sheet microscope
- PMID: 39982748
- PMCID: PMC11874040
- DOI: 10.1073/pnas.2406679122
Volumetric imaging of the 3D orientation of cellular structures with a polarized fluorescence light-sheet microscope
Abstract
Polarized fluorescence microscopy is a valuable tool for measuring molecular orientations in biological samples, but techniques for recovering three-dimensional orientations and positions of fluorescent ensembles are limited. We report a polarized dual-view light-sheet system for determining the diffraction-limited three-dimensional distribution of the orientations and positions of ensembles of fluorescent dipoles that label biological structures. We share a set of visualization, histogram, and profiling tools for interpreting these positions and orientations. We model the distributions based on the polarization-dependent efficiency of excitation and detection of emitted fluorescence, using coarse-grained representations we call orientation distribution functions (ODFs). We apply ODFs to create physics-informed models of image formation with spatio-angular point-spread and transfer functions. We use theory and experiment to conclude that light-sheet tilting is a necessary part of our design for recovering all three-dimensional orientations. We use our system to extend known two-dimensional results to three dimensions in FM1-43-labeled giant unilamellar vesicles, fast-scarlet-labeled cellulose in xylem cells, and phalloidin-labeled actin in U2OS cells. Additionally, we observe phalloidin-labeled actin in mouse fibroblasts grown on grids of labeled nanowires and identify correlations between local actin alignment and global cell-scale orientation, indicating cellular coordination across length scales.
Keywords: biophysical; imaging; inverse problem; polarized fluorescence microscopy.
Conflict of interest statement
Competing interests statement:T.C., Y.W., S.B.M., A.K., R.O., P.J.L.R., and H.S. hold US Patent #11428632.
Figures

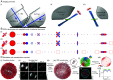
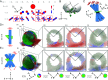


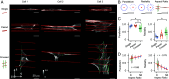
Comment in
-
Painting rich six-dimensional pictures using polarized fluorescence microscopy.Proc Natl Acad Sci U S A. 2025 Apr 8;122(14):e2501914122. doi: 10.1073/pnas.2501914122. Epub 2025 Mar 31. Proc Natl Acad Sci U S A. 2025. PMID: 40163739 Free PMC article. No abstract available.
References
-
- Brasselet S., Alonso M. A., Polarization microscopy: From ensemble structural imaging to single-molecule 3D orientation and localization microscopy. Optica 10, 1486–1510 (2023).
-
- Lakowicz J. R., Principles of Fluorescence Spectroscopy (Springer, New York, ed. 3, 2006).
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

