Finite-Size Scaling in the Ageing Dynamics of the 1 D Glauber-Ising Model
- PMID: 40003136
- PMCID: PMC11854681
- DOI: 10.3390/e27020139
Finite-Size Scaling in the Ageing Dynamics of the 1 D Glauber-Ising Model
Abstract
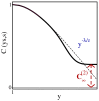
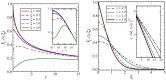
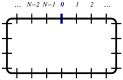
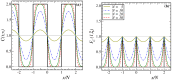
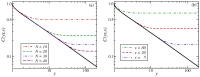
Single-time and two-time correlators are computed exactly in the 1D Glauber-Ising model after a quench to zero temperature and on a periodic chain of finite length N, using a simple analytical continuation technique. Besides the general confirmation of finite-size scaling in non-equilibrium dynamics, this allows for testing the scaling behaviour of the plateau height C∞(2), to which the two-time auto-correlator converges when deep in the finite-size regime.
Keywords: Glauber-Ising model; ageing dynamics; finite-size scaling.
Conflict of interest statement
The author declare no conflicts of interest.
Figures
Similar articles
-
Kibble-Zurek scalings and coarsening laws in slowly quenched classical Ising chains.Phys Rev E. 2024 May;109(5-1):054116. doi: 10.1103/PhysRevE.109.054116. Phys Rev E. 2024. PMID: 38907392
-
Scaling of the linear response in simple aging systems without disorder.Phys Rev E Stat Nonlin Soft Matter Phys. 2004 May;69(5 Pt 2):056109. doi: 10.1103/PhysRevE.69.056109. Epub 2004 May 19. Phys Rev E Stat Nonlin Soft Matter Phys. 2004. PMID: 15244885
-
Comment on "Phase transition in a one-dimensional Ising ferromagnet at zero temperature using Glauber dynamics with a synchronous updating mode".Phys Rev E Stat Nonlin Soft Matter Phys. 2011 Mar;83(3 Pt 1):033101. doi: 10.1103/PhysRevE.83.033101. Epub 2011 Mar 3. Phys Rev E Stat Nonlin Soft Matter Phys. 2011. PMID: 21517548
-
Comparison of voter and Glauber ordering dynamics on networks.Phys Rev E Stat Nonlin Soft Matter Phys. 2005 Jun;71(6 Pt 2):066107. doi: 10.1103/PhysRevE.71.066107. Epub 2005 Jun 10. Phys Rev E Stat Nonlin Soft Matter Phys. 2005. PMID: 16089820
-
Phase transition in a one-dimensional Ising ferromagnet at zero temperature using Glauber dynamics with a synchronous updating mode.Phys Rev E Stat Nonlin Soft Matter Phys. 2010 Sep;82(3 Pt 1):031120. doi: 10.1103/PhysRevE.82.031120. Epub 2010 Sep 14. Phys Rev E Stat Nonlin Soft Matter Phys. 2010. PMID: 21230038
References
-
- Arceri F., Landes F.P., Berthier L., Biroli G. A statistical mechanics perspective on glasses and ageing. In: Meyers R.A., editor. Encyclopedia of Complexity and Systems Science. Springer; Berlin/Heidelberg, Germany: 2021. - DOI
-
- Vincent E. In: Encyclopedia of Condensed Matter Physics. Chakraborty T., editor. Volume 2. Oxford University Press; Oxford, UK: 2024. pp. 371–387. - DOI
-
- Struik L.C.E. Physical Ageing in Amorphous Polymers and Other Materials. Elsevier; Amsterdam, The Netherlands: 1978.
-
- Bray A.J. Theory of Phase Ordering Kinetics. Adv. Phys. 1994;43:357. doi: 10.1080/00018739400101505. - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous

