Protocells Either Synchronize or Starve

Abstract

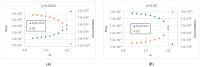
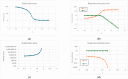
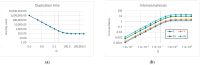
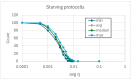
Two different processes take place in self-reproducing protocells, i.e., (i) cell reproduction by fission and (ii) duplication of the genetic material. One major problem is indeed that of assuring that the two processes take place at the same pace, i.e., that they synchronize, which is a necessary condition for sustainable growth. In previous theoretical works, using dynamical models, we had shown that such synchronization can spontaneously emerge, generation after generation, under a broad set of hypotheses about the architecture of the protocell, the nature of the self-replicating molecules, and the types of kinetic equations. However, an important class of cases (quadratic or higher-order self-replication) did not synchronize in the models we had used, but could actually lead to divergence of the concentration of replicators. We show here that this behavior is due to a simplification of the previous models, i.e., the "buffering" hypothesis, which assumes instantaneous equilibrium of the internal and external concentrations of those compounds which can cross the cell membrane. That divergence disappears if we make use of more realistic dynamical models, with finite transmembrane diffusion rates of the precursors of replicators.

Keywords: Fick’s law; chemical kinetics; diffusion rate; self-replication; self-reproduction; transmembrane diffusion.

Figure 1

(a) Asymptotic time required for duplication (i.e., duration of a single generation) and asymptotic replicator concentration at the time of duplication, for low values of the η coefficient. In this situation, the growth of the exponent ν leads to increasingly lower values of replicator concentration and to increasingly higher duplication times (“starvation”). (b) The same variables for higher η value. In this situation, the growth of the exponent ν leads to increasingly higher replicator concentration values and ultimately to divergence, and consequently to increasingly shorter and ultimately vanishing duplication times. The α coefficient is 0.05 in both images.

Figure 2

(a) Time needed for duplication (i.e., duration of a single generation) and (b) internal concentration of replicator and of the precursor at duplication time as exponent ν varies (η = 2.0 × 10⁻⁴, α = 10⁻², D = 10⁻¹⁴). (c,d) The same, but with coefficients that lead to starvation (η = 5.0 × 10⁻⁵, α = 10⁻², D = 10⁻¹⁴).

Figure 3

(a) Duplication time of a protocell composed of two replicators and two precursors that cross the membrane as the diffusion coefficient across the membrane varies—here, D_x = D_y, η_x = 9.0 × 10⁻⁴, η_y = 10⁻³, α_x = 5.0 × 10⁻², α_y = 5.0 × 10⁻². (b) The concentrations at duplication time of replicators and precursors. There are no out-of-sync situations.

Figure 4

Minimum, mean, median, and maximum number of protocells that dilute as the mean value of the reaction coefficients varies (the constants α_i are all set to 0.01). Statistics are calculated on 20 runs involving ensembles of 100 protocells, each protocell containing 15 replicators and the corresponding precursors; protocells that do not starve synchronize. The transition occurs in the narrow interval [0.0005, 0.01]; outside this zone all protocells have the same behavior (starvation, or synchronization).

Figure 5

(a) The behavior of the duplication time in an example of synchronizing protocell, and (b) the corresponding concentrations of internal precursors (α_i set to 0.01, random η_i with mean close to 0.01). All measurements are taken immediately before the time of division. (c,d) The same behaviors in an observed case of supersynchronization (α_i set to 0.01, random η_i with mean close to 0.001—as commented in the main text, the variability of η_i values involves multiplying the desired mean value by, or dividing by, a random coefficient drawn from a uniform distribution in the interval [1.0, 3.0]).

Figure 6

(a) Distribution of duplication times of an ensemble of 5000 protocells, composed of 15 replicators and their precursors (α_i equal to 0.01, random η_i with mean equal to 0.01). Only 15 protocells did not synchronize and therefore are not present in the distribution. (b) Relation at duplication time between the concentrations of a (randomly chosen) replicator and its precursor in the 5985 protocells that synchronized. (c) Concentration distribution of this precursor and (d) of the associated replicator.

Figure 7

(a) Starvation of a protocell composed of 15 replicators: low η_i (α_i equal to 0.01, random η_i with mean equal to 0.014). (b) Divergence of the same protocell: high η_i (α_i equal to 0.01, random η_i with mean equal to 0.032).