Levy Noise Affects Ornstein-Uhlenbeck Memory

Abstract

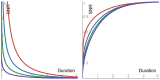
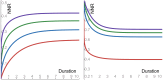
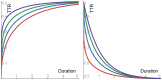
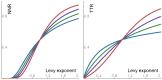
This paper investigates the memory of the Ornstein-Uhlenbeck process (OUP) via three ratios of the OUP increments: signal-to-noise, noise-to-noise, and tail-to-tail. Intuition suggests the following points: (1) changing the noise that drives the OUP from Gauss to Levy will not affect the memory, as both noises share the common 'independent increments' property; (2) changing the auto-correlation of the OUP from exponential to slowly decaying will affect the memory, as the change yields a process with long-range correlations; and (3) with regard to Levy driving noise, the greater the noise fluctuations, the noisier the prediction of the OUP increments. This paper shows that intuition is plain wrong. Indeed, a detailed analysis establishes that for each of the three above-mentioned points, the very converse holds. Hence, Levy noise has a significant and counter-intuitive effect on Ornstein-Uhlenbeck memory.

Keywords: Gauss and Levy noises; Langevin equation; Noah and Joseph effects; Ornstein–Uhlenbeck process; light and heavy tails; memory; short-range and long-range correlations.

Figure 1

The signal-to-noise ratio (SNR) of Equation (14), as a function of the duration $\Delta$ (with parameters $\alpha$ = 1 and $\omega$ = 1). Sub-Cauchy examples are depicted in the left panel, with the following Levy exponents: red 0.5; blue 0.6; green 0.7; purple 0.8. Super-Cauchy and Gauss examples are depicted in the right panel, with the following Levy exponents: red 1.25; blue 1.5; green 1.75; purple 2.

Figure 2

The noise-to-noise ratio (NNR) of Equation (15), as a function of the duration $\Delta$ (with parameter $\alpha$ = 1). Sub-Cauchy examples are depicted in the left panel, with the following Levy exponents: red 0.5; blue 0.6; green 0.7; purple 0.8. Super-Cauchy and Gauss examples are depicted in the right panel, with the following Levy exponents: red 1.25; blue 1.5; green 1.75; purple 2.

Figure 3

The tail-to-tail ratio (TTR), as a function of the duration $\Delta$ (with parameter $\alpha$ = 1). Sub-Cauchy examples are depicted in the left panel, with the following Levy exponents: red 0.5; blue 0.6; green 0.7; purple 0.8. Super-Cauchy examples are depicted in the right panel, with the following Levy exponents: red 1.25; blue 1.5; green 1.75; purple 1.99.

Figure 4

The noise-to-noise ratio (NNR) of Equation (15) and the tail-to-tail ratio (TTR), as functions of the Levy exponent p (with parameter $\alpha$ = 1). The examples are depicted with the following values of the duration $\Delta$: blue −ln(0.2); green −ln(0.4); purple −ln(0.6); red −ln(0.8).