Assessment of Cell Viability in Drug Therapy: IC50 and Other New Time-Independent Indices for Evaluating Chemotherapy Efficacy

Abstract

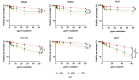
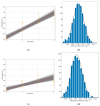
Background/Objectives: Cell viability assays play a crucial role in cancer research and the development of effective treatments. Evaluating the efficacy of conventional treatments across different tumor profiles is essential for understanding patient resistance to chemotherapy and relapse. The IC50 index has been commonly used as a guide in these assays. The idea behind the IC50 index is to compare cell proliferation under treatment with respect to a control population exposed to the same treatment. The index requires normalization to a control and is time dependent. These aspects are disadvantages, as small variations yield different results. In this article, we propose a new method to analyze cell viability assays. Methods: This method involves calculating the effective growth rate for both control (untreated) cells and cells exposed to a range of drug doses for short times, during which exponential proliferation can be assumed. The concentration dependence of the effective growth rate gives a real estimate of the treatment on cell proliferation. A curve fit of the effective growth rate related to concentration yields the concentration corresponding to a given effective growth rate. Results: We use this estimation to calculate the IC50 index and introduce two new parameters (ICr0 and ICrmed) to compare treatment efficacy under different culture conditions or cell lines. Conclusions: In summary, this study presents a new method to analyze cell viability assays and introduces two more precise parameters, improving the comparison and evaluation of efficacy under different conditions.

Keywords: IC50; cell viability; drug resistance; effective growth rate; mathematical model.

Figure A1

The effective growth rate decreases in an exponential dose-dependent manner. The experiment was performed in five cancer cell lines: (a) SW480, (b) SW620, (c) DLD1, (d) HT29, (e) MCF7. A total of 1000 Monte Carlo exponential regressions were performed from the slope distribution obtained in the previous effective growth rate calculation (shown as orange dots). Each gray line corresponds to each bootstrap exponential regression, and the red line is the mean of these fits. The parameters to measure resistance are shown in dashed lines: IC50 (blue), ICr0 (green), and ICrmed (purple).

Figure A2

Distribution of the parameters to measure cell lines’ resistance to drugs. IC50, ICrmed, and ICr0 distributions are shown for SW480, SW620, DLD1, HT29, and MCF7 cancer cell lines.

Figure A3

Diagram of the procedure for the new proposed method.

Figure 1

Exponential growth in the HCT116 cell line in control and treatment conditions. (a) MTT absorbance reading over time fits with an exponential curve in control conditions. The inset shows this growth on a semilogarithmic scale. (b) Exponential fitting of MTT absorbance readings on a semilogarithmic scale for different oxaliplatin concentrations (0, 3.32, and 25 µg/mL). Note that in a semilogarithmic scale plot, data points can be fitted with a linear regression. Three independent experiments were performed, each including three technical replicates.

Figure 2

Concentration dependence of the effective growth rate in the HCT116 cell line. An exponential decrease is shown. The inset shows the same plot on a semilogarithmic scale. Note that in a semilogarithmic scale plot, data points can be fitted with a linear regression. Three independent experiments were performed, each including three technical replicates.

Figure 3

Response to chemotherapy is time dependent in different cell lines. (a) Viability was quantified in six cancer cell lines at three different endpoints (24, 48, and 72 h). Differences were evaluated by the Wilcoxon test. The probability is indicated by * p < 0.05, and ** p < 0.01. (b) IC50 value was calculated by GraphPad Prism and IC50 calculator programs in six cancer cell lines for three endpoints (24, 48, and 72 h). Three independent experiments were performed, each including three technical replicates.

Figure 3

Response to chemotherapy is time dependent in different cell lines. (a) Viability was quantified in six cancer cell lines at three different endpoints (24, 48, and 72 h). Differences were evaluated by the Wilcoxon test. The probability is indicated by * p < 0.05, and ** p < 0.01. (b) IC50 value was calculated by GraphPad Prism and IC50 calculator programs in six cancer cell lines for three endpoints (24, 48, and 72 h). Three independent experiments were performed, each including three technical replicates.

Figure 4

Growth rate calculation and distribution in the HCT116 colorectal cancer cell line. (a) Growth rate calculation for HCT116 control condition. A total of 1000 linear regressions were performed over the paired bootstrap samples of the experimental data (shown as orange dots). Each gray line corresponds to each bootstrap linear regression, and the red line represents the mean of these fits. (b) Distribution of the bootstrap linear regression slopes in HCT116 control data. (c) Growth rate calculation for HCT116 with oxaliplatin at a 1.56 µg/mL concentration. (d) Distribution of the bootstrap linear regression slopes in HCT116 with oxaliplatin at a 1.56 µg/mL concentration. Three independent experiments were performed, each including three technical replicates.

Figure 5

The effective growth rate decreases in an exponential dose-dependent manner in the HCT116 cell line. A total of 1000 Monte Carlo exponential regressions were performed from the slope distribution obtained in the previous effective growth rate calculation (shown as orange dots). Each gray line corresponds to each bootstrap exponential regression, and the red line is the mean of these fits. The parameters to measure resistance are shown in dashed lines: IC50 (blue), ICr0 (green), and ICrmed (purple).

Figure 6

Distribution of the parameters to measure cell lines’ resistance to drugs. IC50 (a) ICrmed (b) and ICr0 (c) distributions are shown for the HCT116 cell line.