Woodward and Hoffmann on Secondary Orbital Interactions. How to Make a Fine Two-Course Meal from Leftovers
- PMID: 40012337
- PMCID: PMC12461183
- DOI: 10.1002/tcr.202400051
Woodward and Hoffmann on Secondary Orbital Interactions. How to Make a Fine Two-Course Meal from Leftovers
Abstract
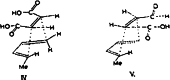
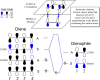
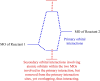
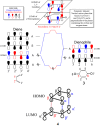
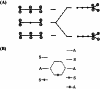
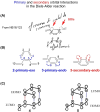
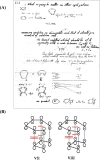
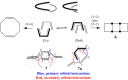
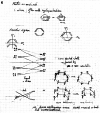
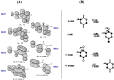
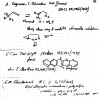
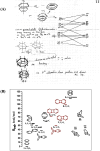
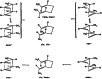
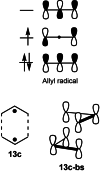
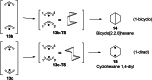
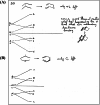
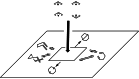
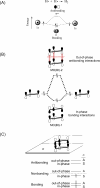
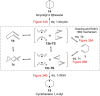
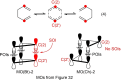
In 1965, R. B. Woodward and Roald Hoffmann published five communications in the Journal of the American Chemical Society that formed the basis for what has been known as the Woodward and Hoffmann (W-H) rules. The last two of these communications applied secondary molecular orbital interactions - that is, interactions that involved atomic orbitals removed from the primary reaction centers - to explain the so-called Alder endo-exo rule of maximum overlap of orbitals for regiochemistry in the Diels-Alder reaction and the then recently noted preference of the chair orientation over the boat orientation in the Cope reaction. This publication presents the back stories of these latter two W-H communications, based on a comprehensive examination of Hoffmann's laboratory notebooks, more than 100 hours of interviews with Hoffmann, interviews with other chemists, and documents found in both Hoffmann's and Woodward's archives.
Keywords: Woodward-Hoffmann rules; history of chemistry; mechanism of pericyclic reactions; molecular orbital theory; secondary orbital interactions.
© 2024 The Author(s). The Chemical Record published by The Chemical Society of Japan and Wiley-VCH GmbH.
Figures
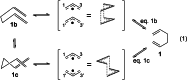


































References
-
- Woodward R. B., Hoffmann R., J. Am. Chem. Soc. 1965, 87, 395–397, 10.1021/ja01080a054. - DOI
-
- Hoffmann R., Woodward R. B., J. Am. Chem. Soc. 1965, 87, 2046–2048, 10.1021/ja01087a034. - DOI
-
- Woodward R. B., Hoffmann R., J. Am. Chem. Soc. 1965, 87, 2511–2513, 10.1021/ja01089a050. - DOI
-
- Hoffmann R., Woodward R. B., J. Am. Chem. Soc. 1965, 87, 4388–4389, 10.1021/ja00947a033. - DOI
-
- Hoffmann R., Woodward R. B., J. Am. Chem. Soc. 1965, 87, 4389–4390, 10.1021/ja00947a034. - DOI
Publication types
LinkOut - more resources
Full Text Sources

