Understanding Nash epidemics

Abstract

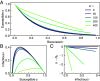
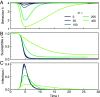
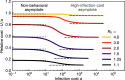
Faced with a dangerous epidemic humans will spontaneously social distance to reduce their risk of infection at a socioeconomic cost. Compartmentalized epidemic models have been extended to include this endogenous decision making: Individuals choose their behavior to optimize a utility function, self-consistently giving rise to population behavior. Here, we study the properties of the resulting Nash equilibria, in which no member of the population can gain an advantage by unilaterally adopting different behavior. We leverage an analytic solution that yields fully time-dependent rational population behavior to obtain, 1) a simple relationship between rational social distancing behavior and the current number of infections; 2) scaling results for how the infection peak and number of total cases depend on the cost of contracting the disease; 3) characteristic infection costs that divide regimes of strong and weak behavioral response; 4) a closed form expression for the value of the utility. We discuss how these analytic results provide a deep and intuitive understanding of the disease dynamics, useful for both individuals and policymakers. In particular, the relationship between social distancing and infections represents a heuristic that could be communicated to the population to encourage, or "bootstrap," rational behavior.

Keywords: control theory; epidemiology; game theory; mathematical modeling; mean-field games.

Fig. 1.

Direct plots of the analytic solution. (A) The analytic solution of the Nash equilibrium social distancing problem as obtained in Eq. 23 as a function of the recovered $r$ for an exemplary range of infection costs $\alpha$ and $R_0=4$. Initial conditions here and in all following figures are set to $r_0={10}^{-6}$ and $i_0=3·{10}^{-6}$. (B) The fraction of infectious $i$ as a function of the susceptible $s$ for the same range of $\alpha$. (C) Deviation of the social distancing behavior $k$ from the pre-epidemic default $R_0$ as a function of $i$, emphasizing their linear relationship as established in Eq. 20.

Fig. 2.

Analytic solution as a function of time. (A) Equilibrium social activity behavior of the population $k(t)$ and corresponding dynamics of the disease (B) $s$ and (C) $i$ for an exemplary range of infection costs $\alpha$ and $R_0=4$. Since infections incur a cost, the equilibrium behavior seeks to avoid excessive infections by self-organized social distancing. The higher the cost, the more reduced social activity $k$ becomes.

Fig. 3.

Scaling. (A) Excess cases $\epsilon (\alpha ,R_0)$ vs. infection cost $\alpha$ for a range of basic reproduction numbers $R_0$. The high infection cost asymptotes, see Eq. 29, are shown as dashed lines and the crossover costs ${\alpha }_{\mathit{ex}}^{\star }$, see Eq. 32, as black stars. Inset: The data collapse onto the low and high infection cost asymptotes by rescaling the cost $\alpha$ with the crossover cost ${\alpha }_{\mathit{ex}}^{\star }$, see Eq. 32, while rescaling $\epsilon (\alpha ,R_0)$ with its nonbehavioral limit, see Eq. 27. (B) The infection peak $\widehat{i}$ vs. $\alpha$ for a range of $R_0$. The high infection cost asymptotes, see Eq. 30, are shown as dashed lines and the crossover costs ${\alpha }_{\mathit{peak}}^{\star }$, see Eq. 33, as gray stars. Inset: The data collapse onto the low and high infection cost asymptotes by rescaling the cost $\alpha$ with the crossover cost ${\alpha }_{\mathit{peak}}^{\star }$, Eq. 33, while rescaling the peak height with its nonbehavioral limit, see Eq. 28.

Fig. 4.

Behavioral response. Characterization of the Nash equilibrium response in the $R_0$—$\alpha$ parameter space. On the high $R_0$—low-$\alpha$ side of the line, the behavior is well represented by the nonbehavioral limit, in which it is not rational to significantly modify one’s behavior. On the low $R_0$—high infection cost side, it is rational to strongly modify one’s behavior. The lines describing the crossover are given by the critical costs ${\alpha }_{\mathit{ex}}^{\star }$ for the transition in the excess cases, see Eq. 32, and/or ${\alpha }_{\mathit{peak}}^{\star }$ for the transition in the infection peak, see Eq. 33. The parameter values used for some of the curves in Figs. 1 and 2 are marked by analogously colored dots.

Fig. 5.

Cost of the epidemic. Total epidemic cost relative to the cost of an infection, $-U/\alpha$, as a function of infection cost $\alpha$ under equilibrium social distancing. The corresponding nonbehavioral, Eq. 35, and high-infection-cost asymptotes, Eq. 36, are indicated by dotted and dashed lines, respectively.