Electrostatics of salt-dependent reentrant phase behaviors highlights diverse roles of ATP in biomolecular condensates

Abstract

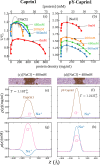
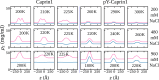
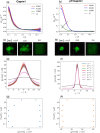
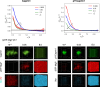
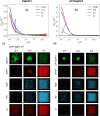
Liquid-liquid phase separation (LLPS) involving intrinsically disordered protein regions (IDRs) is a major physical mechanism for biological membraneless compartmentalization. The multifaceted electrostatic effects in these biomolecular condensates are exemplified here by experimental and theoretical investigations of the different salt- and ATP-dependent LLPSs of an IDR of messenger RNA-regulating protein Caprin1 and its phosphorylated variant pY-Caprin1, exhibiting, for example, reentrant behaviors in some instances but not others. Experimental data are rationalized by physical modeling using analytical theory, molecular dynamics, and polymer field-theoretic simulations, indicating that interchain ion bridges enhance LLPS of polyelectrolytes such as Caprin1 and the high valency of ATP-magnesium is a significant factor for its colocalization with the condensed phases, as similar trends are observed for other IDRs. The electrostatic nature of these features complements ATP's involvement in π-related interactions and as an amphiphilic hydrotrope, underscoring a general role of biomolecular condensates in modulating ion concentrations and its functional ramifications.

Keywords: biochemistry; chemical biology; field-theoretic simulation; intrinsically disordered proteins; liquid-liquid phase separation; molecular biophysics; molecular dynamics; none; phosphorylation; random phase approximation; structural biology.

Figure 1.. rG-RPA+FH theory predictions rationalize different salt dependence of Caprin1 and pY-Caprin1 LLPS.

(a, b) Vertical lines indicate the sequence positions (horizontal variable) of positively charged residues (blue) and negatively charged residues or phosphorylated tyrosines (red) for (a) Caprin1 and (b) pY-Caprin1. (c, d) rG-RPA+FH coexistence curves (phase diagrams, continuous curves color-coded for the NaCl concentrations indicated) agree reasonably well with experiment (dots, same color code). The grey arrows in (c, d) highlight that when [NaCl] increases, LLPS propensity increases for (c) Caprin1 but decreases for (d) pY-Caprin1. As described in our prior RPA+FH and rG-RPA+FH formulations (Lin et al., 2016; Lin et al., 2020), the theoretical coexistence curves shown in (c, d) are determined by fitting an effective relative permittivity ${\displaystyle {ϵ}_{\mathrm{r}}}$ as well as the enthalpic and entropic parts of a FH parameter ${\displaystyle \chi (T)={ϵ}_h/T^{\ast }+{ϵ}_s}$ to experimental data. For the present Caprin1 and pY-Caprin1 systems, the fitted ${\displaystyle {ϵ}_{\mathrm{r}}=80.5}$, which is remarkably close to that of bulk water ${\displaystyle ({ϵ}_{\mathrm{r}}\approx 78.5)}$. The fitted ${\displaystyle ({ϵ}_h,{ϵ}_s)}$ is (1.0, 0.0) for Caprin1 and (1.0, −1.5) for pY-Caprin1. These fitted energetic parameters are equivalent (Lin et al., 2016) to ${\displaystyle \mathrm{\Delta }H\approx -1.1\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}}$ and ${\displaystyle \mathrm{\Delta }S=0.0}$ for forming a residue-residue contact in the Caprin1 system (c) (i.e., it is enthalpically favorable), and ${\displaystyle \mathrm{\Delta }H\approx -1.1\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}}$ and ${\displaystyle \mathrm{\Delta }S\approx -3.0\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}{\mathrm{l}}^{-1}{\mathrm{K}}^{-1}}$ for forming a residue-residue contact in the pY-Caprin1 system (d) (i.e., it is enthalpically favorable and entropically unfavorable).

Figure 2.. rG-RPA+FH theory rationalizes [NaCl]-modulated reentrant phase behavior of Caprin1.

In each salt-protein phase diagram (${\displaystyle T=300}$ K), tielines (dashed) connect coexisting phases on the boundary (magenta curve) of the cyan-shaded coexistence region. For clarity, zoomed-in views of the grey-shaded part in (a, c, e, g, i, k) are provided by the plots to the right, i.e., (b, d, f, h, j, l), respectively. The solid inclined lines in (g, h, k, l) mark the minimum counterion concentrations required for overall electric neutrality. Results are shown for monovalent cation and anion with Caprin1 (a, b) or pY-Caprin1 (c, d); or monovalent cation and divalent anion with Caprin1 (e–h); or divalent cation and tetravalent anion with Caprin1 (i–l). Cation-modulated reentrant phase behaviors is seen for a wide concentration range for Caprin1 in (a, b) but only a very narrow range of high Caprin1 concentrations in (e, f, i, j). The ${\displaystyle ({ϵ}_h,{ϵ}_s)}$ values for computing the phase diagrams here for Caprin1 and pY-Caprin1, respectively, are the same as those used for Figure 1c and d.

Figure 3.. Experimental demonstration of [ATP-Mg]- and [NaCl]-modulated reentrant phase behavior for Caprin1.

(a) Turbidity quantified by optical density at 600 nm (OD600, normalized by peak value) to assess Caprin1 LLPS propensity at [Caprin1]=200 μM [for ATP-Mg dependence (red), bottom scale] or [Caprin1]=300 μM [for NaCl dependence (blue), top scale], measured at room temperature (∼23 °C). Error bars are one standard deviations of triplicate measurements, which in most cases was smaller than the plotting symbols. The ATP-Mg dependence seen here for 200 μM Caprin1 is similar to the results for 400 μM Caprin1 (Figure 6C of Kim et al., 2021). (b) Microscopic images of Caprin1 and pY-Caprin1 at varying [ATP-Mg] at room temperature, showing reentrant behavior for Caprin1 but not for pY-Caprin1. Each sample contains 200 μM of either Caprin1 or pY-Caprin1, with 1% of either Caprin1-Cy5 or pY-Caprin1-Cy5 (labeled with Cyanine 5 fluorescent dye) added for visualization, in a 25 mM HEPES buffer at pH 7.4. Scale bars represent 10 μm.

Figure 4.. Explicit-ion coarse-grained MD rationalizes [NaCl]-modulated reentrant behavior for Caprin1 and lack thereof for pY-Caprin1.

(a) Simulated phase diagrams (binodal curves) of Caprin1 at different temperatures plotted in units of ${\displaystyle T_{\mathrm{c}\mathrm{r}}^0}$ (see text). Symbols are simulated data points. Continuous curves are guides for the eye. Grey arrow indicates variation in [NaCl]. (b) Same as (a) but for pY-Caprin1. (c) A snapshot showing phase equilibrium between dilute and condensed phases of Caprin1 (brown chains) immersed in Na⁺ (blue) and Cl^– (red) ions simulated at [NaCl]=480 mM. (d) A similar snapshot for pY-Caprin1. (e, f) Mass density profiles, ${\displaystyle \rho (z)}$ (in units of mg/ml), of Na⁺, Cl^–, and (e) Caprin1 or (f) pY-Caprin1 along the elongated dimension ${\displaystyle z}$ of the simulation box showing variations of Na⁺ and Cl^– concentrations between the protein-dilute phase (low ${\displaystyle \rho }$ for protein) and protein-condensed phase (high ρ for protein) at the simulation temperatures indicated. (g, h) Corresponding zoomed-in concentration profiles ${\displaystyle \rho (z)}$ in units of mM for Na⁺ and Cl^–. Additional mass density profiles for [NaCl]=200 mM and 400 mM are provided in Appendix 1—figure 3.

Figure 5.. Counterions can stabilize Caprin1 condensed phase by favorable bridging interactions.

(a) Snapshot from explicit-ion coarse-grained MD under LLPS conditions for Caprin1, showing the spatial distributions of Caprin1, Na⁺, and Cl^– (as in Figure 4c). The three components of the same snapshot are also shown separately in (b) Caprin1, (c) Na⁺, and (d) Cl^–. (e) A zoomed-in view of the condensed droplet corresponding to the green box in (a), now with a black background and a different color scheme. (f) A further zoomed-in view of the part enclosed by the green box in (e) focusing on two interacting Caprin1 chains. A Cl^– ion (pink bead indicated by the arrow) is seen interacting favorably with two arginine residues (blue beads) on the two Caprin1 chains (whose uncharged residues are colored differently by yellow or orange, lysine and aspartic acids in both chains are depicted, respectively, in magenta and red).

Figure 6.. Counterion interactions in polyelectrolytic Caprin1.

Shown distributions are averaged from 4000 equilibrated coarse-grained MD snapshots of 100 Caprin1 chains and 1300 Cl^– counterions under phase-separation conditions (${\displaystyle T/T_{\mathrm{c}\mathrm{r}}^0=160/193=0.829}$) in a 115×115×1610 ų simulation box in which essentially all Caprin1 chains are in a condensed droplet. (a) Radial distribution function of Cl^– around a positively charged arginine residue (Arg⁺). (b) A zoomed-in view of Figure 5f showcasing a putative bridging configuration with a Cl^– interacting favorably with a pair of Arg⁺s on two different Caprin1 chains. Configurational geometry is characterized by Arg⁺--Arg⁺ distance ${\displaystyle R}$ and the distance ${\displaystyle d}$ of the Cl^– from the line connecting the two Arg⁺s. (c) Distribution of putative bridging interaction configurations with respect to ${\displaystyle R}$. Numbers of true bridging, neutralizing, and intermediate configurations are, respectively, in blue, green and orange. (d, e) Heat maps of two-dimensional projections of spatial distributions of Cl^– around two Arg⁺s satisfying the putative bridging interaction conditions among the MD snapshots. (f, g) Corresponding projected distributions of isolated Arg⁺--Cl^–--Arg⁺ Boltzmann-averaged systems at model temperature ${\displaystyle T}$. Here, ${\displaystyle P(x,d)}$ is the total density of Cl^– on a circle of radius ${\displaystyle |d|}$ perpendicular to the heat map at horizontal position ${\displaystyle x}$ (d, f); thus the average Cl^– density at a given point ${\displaystyle (x,d)}$ is ${\displaystyle P(x,d)/2\pi |d|}$, the patterns of which are exhibited by ${\displaystyle P(x,d)/|d|}$ heat maps in (e, g). ${\displaystyle P(x,d)}$ is symmetric with respect to ${\displaystyle d\leftrightarrow -d}$ by construction, i.e., ${\displaystyle P(x,d)=P(x,-d)}$. In each heat map, the size and (ranges of) positions of model Arg⁺s are indicated by blue circles; the size and the position or one of two positions (at ±d) of maximum Cl^– density is indicated by a magenta circle. The MD-simulated distributions of the condensed system (d, e) are quite similar to the theory-computed isolated system (f, g) for ${\displaystyle R\lesssim 14}$ Å, indicating that individual bridging interactions in the crowded Caprin1 condensates may be understood approximately by the electrostatics of an isolated, three-bead Arg⁺--Cl^–--Arg⁺ system. For larger ${\displaystyle R}$, the heat maps in (f, g) and (d, e) are not as similar because some of the configurations in the isolated system (f, g) are precluded by the requirement that Arg⁺--Cl^– distance < 11 Å for putative bridging interactions in (d, e).

Figure 7.. Explicit-ion coarse-grained MD rationalizes [NaCl]-modulated phase behavior for RtoK variants of Caprin1.

Four variants studied experimentally (Wong et al., 2020) are simulated: (a) 15Rto15K, in which 15 R’s in the WT Caprin1 IDR are substituted by K, (b) 4Rto4K_N, (c) 4Rto4K_M, and (d) 4Rto4K_C, in which 4 R’s are substituted by K in the (b) N-terminal, (c) middle, and (d) C-terminal regions, respectively. Top panels show positions of the R (dark blue) and K (cyan) along the Caprin1 IDR sequence. Lower panels are phase diagrams in the same style as Figure 4. The phase diagrams for WT Caprin1 from Figure 4a are included as continuous curves with no data points in (a) for comparison.

Figure 8.. FTS rationalizes experimental observation of Caprin1-ATP interactions.

(a) The 6-bead model for (ATP-Mg)²⁻ and the single-bead models for monovalent salt ions used in the present FTS. (b–e) Normalized protein-protein correlation functions at three [(ATP-Mg)²⁻] values (b, c) and protein-ion correlation functions (Equation 7) at [(ATP-Mg)²⁻]/b⁻³ = 0.03 (d, e) for Caprin1 (b, d) and pY-Caprin1 (c, e), computed for Bjerrum length ${\displaystyle l_{\mathrm{B}}=7b}$. Horizontal dashed lines are unity baselines (see text). (f) Values of position-specific integrated correlation ${\displaystyle {\mathcal{G}}_{\mathrm{p}\mathrm{q}}^{(i)}/{\rho }_{\mathrm{p},i}^0{\rho }_{\mathrm{q}}^0}$ (left vertical axis) correspond to the relative contact frequencies between individual residues labeled by i along the Caprin1 IDR sequence with q = (ATP-Mg)²⁻, Na⁺, or Cl⁻ under the same conditions as (d) (Equation 9) (color symbols). Included for comparison are experimental NMR volume ratios ${\displaystyle V/V_0}$ data on site-specific Caprin1-ATP association (Kim et al., 2021). ${\displaystyle V/V_0}$ decreases with increased contact probability, although a precise relationship is yet to be determined. Thus, the plotted ${\displaystyle 1-V/V_0}$ (grey data points, right vertical scale) is expected to correlate with contact frequency.

Figure 9.. FTS rationalizes colocalization of ATP-Mg with the Caprin1 condensate.

FTS snapshots are from simulations at ${\displaystyle l_{\mathrm{B}}=7b}$ (same as that for Figure 8). Spatial distributions of real positive parts of the density fields for the protein (a, b), (ATP-Mg)²⁻ (c, d), Na⁺ (e, f), and Cl^– (g, h) components are shown by three snapshots each for Caprin1 (left panels) and pY-Caprin1 (right panels) at different [(ATP-Mg)²⁻] values as indicated. Colocalization of (ATP-Mg)²⁻ with the Caprin1 condensed droplet is clearly seen in the [(ATP-Mg)²⁻]/b⁻³ = 0.03 panel of (c).

Appendix 1—figure 1.. Sequences of wildtype (WT) and variant Caprin1 IDRs studied in this work.

Positively charged arginine (R) and lysine (K) residues are shown, respectively, in dark and light blue, negatively charged aspartic acid (D) residues and phosphorylated tyrosines (pY) are shown in red. Other residues are in black.

Appendix 1—figure 2.. Mass spectrometry analysis of pY-Caprin1.

The graph plots deconvoluted mass (in atomic mass units, amu) on the horizontal axis against intensity (normalized counts) on the vertical axis. Peaks are observed at 11,510 Da (+5 phosphate groups,+5 P), 11,590 Da (+6 P), and 11,670 Da (+7 P). Asterisks mark the peaks of pY-Caprin1 with oxidized methionine residues.

Appendix 1—figure 3.. Explicit-ion coarse-grained molecular dynamics simulation of salt and counterion mass density profiles in protein-dilute and protein-condensed phases of Caprin1 and pY-Caprin1.

Mass density profile ρ_z for Na⁺ (blue) and Cl^– (red) in units of mg/ml for the Caprin1 (three left columns) and pY-Caprin1 (three right columns) systems are shown as in Figure 4e and f of the maintext. Regions with elevated [Cl^–] here coincide with positions of the condensed protein droplets. Overall [NaCl] values used for the simulations are provided on the right.

Appendix 1—figure 4.. FTS models for Caprin1 and pY-Caprin1 with only Na⁺and Cl^– but no ATP-Mg.

(a, b) Protein-protein correlation functions [maintext Equation 7] for Caprin1 (a) and pY-Caprin1 (b) at three different [Na⁺]s, color coded in units of b^–3 as provided. In each figure, the baseline value of protein-protein correlation function ${\displaystyle ({\rho }_{\mathrm{p}}^0{)}^2}$ (square of overall protein concentration) is marked by the horizontal dashed line. Phase separation is indicated by large-r correlation function values falling below this baseline. The grey arrow in (b) marks the direction of increasing [Na⁺]. (c, d) Field snapshots for the Caprin1 (c) and pY-Caprin1 (d) systems at different [Na⁺] values. The above results are obtained at Bjerrum length ${\displaystyle l_{\mathrm{B}}=7b}$. (e–h) Results from an alternate FTS model using an elongated simulation box similar to that utilized for our explicit-ion coarse-grained MD. (e, f) Protein concentration profiles computed at different NaCl concentrations for Caprin1 (e) and pY-Caprin1 (f) [color code for density profiles provided in f]. (g, h) salt-protein phase diagrams obtained from the concentration profiles in (e, f) for Caprin1 (g) and pY-Caprin1 (h).

Appendix 1—figure 5.. Alternate FTS models for Caprin1 and pY-Caprin1 with (ATP-Mg)^2– and either Na⁺ or Cl^– (but not both) to maintain overall electric neutrality.

For Caprin1, which has a net positive charge, (ATP-Mg)^2– is the counterion. Depending on [(ATP-Mg)^2–], either Cl^– is included as an additional counterion (when [(ATP-Mg)^2–] is insufficient to balance the positive charges on Caprin1), or Na⁺ is included as salt ion (when [(ATP-Mg)^2–] overcompensates the positive charges on Caprin1). Na⁺ and Cl^– are not included together in this simplified formulation. For pY-Caprin1, which has a net negative charge, Na⁺ is used as counterion, and its concentration depends on [(ATP-Mg)^2–] in such a way that electric neutrality of the entire system is maintained. Top panels: protein-protein correlation functions at different concentrations of (ATP-Mg)^2– (color coded in units of b^–3 as provided). Horizontal dashed lines are ${\displaystyle ({\rho }_{\mathrm{p}}^0{)}^2}$ baselines as in Appendix 1—figure 4a, b. Grey arrows indicate increasing [(ATP-Mg)^2–]. Bottom panels: Field snapshots for system components at different [(ATP-Mg)^2–] (as indicated) for the Caprin1 (left panels) and pY-Caprin1 (right panels) systems. Results here are obtained at ${\displaystyle l_{\mathrm{B}}=7b}$.

Appendix 1—figure 6.. Alternate FTS models for Caprin1 or pY-Caprin1 with ATP^4–, Mg²⁺, Na⁺ and Cl^–, wherein (ATP-Mg)^2– is assumed to be fully dissociable.

Results are obtained for ${\displaystyle l_{\mathrm{B}}=7b}$ and presented in the same style as that in Figure 8b, c and Figure 9 of the maintext as well as Appendix 1—figure 5.