Comparing computational times for simulations when using PBPK model template and stand-alone implementations of PBPK models

Abstract

Introduction: We previously developed a PBPK model template that consists of a single model "superstructure" with equations and logic found in many physiologically based pharmacokinetic (PBPK) models. Using the template, one can implement PBPK models with different combinations of structures and features.

Methods: To identify factors that influence computational time required for PBPK model simulations, we conducted timing experiments using various implementations of PBPK models for dichloromethane and chloroform, including template and stand-alone implementations, and simulating four different exposure scenarios. For each experiment, we measured the required computational time and evaluated the impacts of including various model features (e.g., number of output variables calculated) and incorporating various design choices (e.g., different methods for estimating blood concentrations).

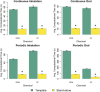
Results: We observed that model implementations that treat body weight and dependent quantities as constant (fixed) parameters can result in a 30% time savings compared with options that treat body weight and dependent quantities as time-varying. We also observed that decreasing the number of state variables by 36% in our PBPK model template led to a decrease of 20-35% in computational time. Other factors, such as the number of output variables, the method for implementing conditional statements, and the method for estimating blood concentrations, did not have large impacts on simulation time. In general, simulations with PBPK model template implementations of models required more time than simulations with stand-alone implementations, but the flexibility and (human) time savings in preparing and reviewing a model implemented using the PBPK model template may justify the increases in computational time requirements.

Conclusion: Our findings concerning how PBPK model design and implementation decisions impact computational speed can benefit anyone seeking to develop, improve, or apply a PBPK model, with or without the PBPK model template.

Keywords: PBPK model; computational timing; pharmacokinetics; risk assessment; template model.

FIGURE 1

Mapping a PBPK model for dichloromethane (DCM) to the PBPK model template superstructure. The model template superstructure includes multiple tissue compartments and features that commonly appear in published PBPK models, so to implement a particular chemical-specific PBPK model using the PBPK model template, the desired structure must be mapped onto the model template superstructure by setting the appropriate parameters. Unused parameters are set to zero, and for unused compartments, the respective blood flows are set to zero. The mapping of the U.S. EPA (2011) PBPK model for DCM is shown here by using lighter colored arrows, boxes, and text for parameters and compartments that are “switched off” or set to zero.

FIGURE 2

Mapping a PBPK model for chloroform (CF) to the PBPK model template superstructure. To implement the Sasso et al. (2013) PBPK model for CF, we mapped the existing model structure to the PBPK model template superstructure by setting the appropriate parameters. Unused parameters are set to zero, and for unused compartments, the respective blood flows are set to zero. The mapping of the published CF model to the model template superstructure is shown here by using lighter colored arrows, boxes, and text for parameters and compartments that are “switched off” or set to zero.

FIGURE 3

Comparison of the computational time required to run a simulation using the template implementation of a given chemical-specific PBPK model and that required using a stand-alone implementation of that model. The height of each bar represents the mean computational time ( $n=10$ ) to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). Darker and lighter bars represent times required for the PBPK model template implementation and the stand-alone model implementation, respectively, for each chemical. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times for the template and stand-alone model implementations. A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 4

Comparison of the computational times required for simulations with template implementations of the given PBPK model (“DCM” or “CF”) that use different options to implement conditional statements. The height of each bar represents the mean computational time ( $n=10$ ) to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). Darker and lighter bars represent times required for the model implementations using ternary conditional operators (“Ternary Ops”) and multiplicative logical switches (“Switches”), respectively, for all conditional statements. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required for the implementations using ternary conditional operators and multiplicative logical switches. A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 5

Comparison of the computational times required for simulations using a template implementation of a given PBPK model (“DCM” or “CF”) with different numbers of output time points (50, 100, or 500) to be returned with the simulation results. For each exposure scenario, the solid and dashed lines indicate the results for the average computational times required to perform 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations using the template implementation of the DCM and CF PBPK models, respectively.

FIGURE 6

Comparison of the computational times required for simulations using a template implementation of a given PBPK model (“DCM” or “CF”) with different numbers of outputs (i.e., calculated quantities not including state variables) returned with the simulation results. The height of each bar represents the mean computational time ( $n=10$ ) required to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). Darker and lighter bars represent times required using the original PBPK model template (with 105 output variables) and an alternative version of the PBPK model template with fewer (76) output variables. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required for simulations using implementations based on the original PBPK model template and the version of the template with fewer output variables. A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 7

Comparison of the computational times required for simulations using template implementations of a given PBPK model (“DCM” or “CF”) when body weight is treated as time-varying (“BW Input”) or constant (“BW Fixed”) parameters and body weight dependent quantities are treated as possibly dynamically changing throughout the simulation (“Params Dyn”) or are calculated just once during an initialization step (“Params Init”). The height of each bar represents the mean computational time ( $n=10$ ) required to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). In each panel, the darkest bar represents the computational time for the implementation in which body weight is treated as a time-varying input parameter, the middle bar represents the computational time for the implementation in which body weight is treated as a constant parameter but dependent quantities are calculated at each step of the integration algorithm, and the lightest bar represents the computational time for the implementation in which body weight is treated as a constant parameter and dependent quantities are calculated only once per simulation. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required when using the implementation in which body weight is treated as a time-varying input parameter and an alternative implementation in which body weight is treated as a constant parameter. Note, for the option in which body weight is treated as a time-varying input parameter, the body weight parameter had a constant value during the entire simulation and was described by a constant-valued input table. A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 8

Comparison of the computational times required for simulations using template implementations of a given PBPK model (“DCM” or “CF”) that include (“Original”) or do not include (“No Zero States”) equations for compartments that are deactivated in the full PBPK model template to more efficiently match the chemical-specific PBPK model. The height of each bar represents the mean computational time ( $n=10$ ) required to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). Darker and lighter bars represent times required using the original PBPK model template (with 53 state variables) and an alternative version of the PBPK model template without the deactivated state variables (which had 34 state variables for the DCM model and 33 state variables for the CF model), respectively. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required when using the original PBPK model template and the version without the deactivated state variables. A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 9

Comparison of the computational times required for simulations using template implementations of a given PBPK model (“DCM” or “CF”) that utilize different (already existing within the model template) options (“SS Approx” or “No SS Approx”) for modeling blood compartments. The heigh of each bar represents the mean computational time ( $n=10$ ) required to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). Darker and lighter bars represent times required when using steady state approximations or state variables, respectively, to represent the concentrations (or amounts) of chemical in the venous and arterial blood. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required when using steady state approximations or state variables to represent blood compartment concentrations (or amounts). A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.

FIGURE 10

Comparison of the computational times required for simulations using template implementations of a given (“DCM” or “CF”) model that utilize different options (“No Lung” vs. “Lung” and “GE SS” vs. “GE Not SS”) for modeling the lung compartment and the gas exchange region. The heigh of each bar represents the mean computational time ( $n=10$ ) required to complete 10 k (for continuous exposures) or 1 k (for periodic exposures) simulations for each model implementation. Error bars show means ± standard deviations in computational time ( $n=10$ ). In each panel, the darkest bar represents the computational time for the implementation with no explicit lung compartment and a steady state approximation of the concentration of chemical in the gas exchange region, the middle bar represents the computational time for the implementation with an explicit lung compartment and a steady state approximation of the concentration of chemical in the gas exchange region, and the lightest bar represents the computational time for the implementation with an explicit lung compartment with terms describing the rates of inhalation and exhalation of chemical. An asterisk above a bar indicates that there was a statistically significant difference ( $p<0.05$ ) between the average computational times required when using the implementations with or without an explicit lung compartment. Note that for DCM, when using the implementation without an explicit lung compartment, lung metabolism was excluded from the model (even though such metabolism is an inherent feature of the original DCM PBPK model). A table showing means and standard deviations for computational times for these simulation experiments is provided in the Supplementary Material.