Thermo-responsive jamming by particle shape change
- PMID: 40055334
- PMCID: PMC11889120
- DOI: 10.1038/s41467-025-57475-5
Thermo-responsive jamming by particle shape change
Abstract
Granular materials transition between unjammed (deformable) and jammed (rigid) states when adjusting their packing density. Here, we report on experiments demonstrating that the same kind of phase transition can be alternatively achieved through temperature-controlled particle shape change. Using a confined system of randomly-packed rod-like particles made of shape memory alloy (SMA), we exploit that shape recovery of these bent rods with rising temperature at a constant packing density leads to a jammed state. The responsible physical processes are elucidated with numerical simulations based on the Discrete Element Method. As an exemplary application of the uncovered mechanism, we engineer a smart clamp that can actively grip or release an object through the thermo-induced jamming or unjamming of the granular material, and robustly so under cyclic temperature changes. In the jammed state, its load-bearing capability surpasses the total SMA weight by a tunable margin, up to over 800-fold. The clamping design paves the way towards a new kind of functional devices based on the thermo-responsive jamming of shape memory granular materials.
© 2025. The Author(s).
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures





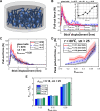
References
-
- Guo, Y. & Curtis, J. S. Discrete element method simulations for complex granular flows. Annu. Rev. Fluid Mech.47, 21–46 (2015).
-
- Shen, Z. & Lintuvuori, J. S. Collective flows drive cavitation in spinner monolayers. Phys. Rev. Lett.130, 188202 (2023). - PubMed
-
- Vicsek, T. & Zafeiris, A. Collective motion. Phys. Rep.517, 71–140 (2012).
-
- Junot, G., De Corato, M. & Tierno, P. Large scale zigzag pattern emerging from circulating active shakers. Phys. Rev. Lett.131, 068301 (2023). - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

