Solvation, geometry, and assembly of the tobacco mosaic virus

Abstract

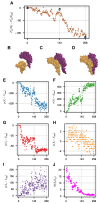
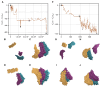
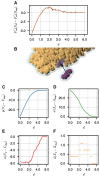
Biological self-assembly is a fundamental aspect in the development of complex structures in nature. A paradigm for such a process is the assembly of tobacco mosaic virus (TMV) capsid proteins into helical rods around the viral genome. The self-assembly process of the virus is typically modelled through attractive interactions between protein subunits, however capsid proteins also interact with their aqueous environment through solvation free energy. An open question is what role solvation plays in virus self-assembly. Here, we show that a purely geometric model of nonpolar solvation free energy, the morphometric approach, is sufficient to simulate the assembly of up to three protein subunits of TMV. The lowest solvation free energy states we find in a geometric simulation setting are remarkably close to the correctly assembled states of various experimentally determined structures. This demonstrates that van der Waals forces and entropic considerations are sufficient to guide assembly in the absence of attractive interactions between protein subunits. It further illustrates the impact of the morphometric approach as a computationally efficient model for nonpolar solvation free energy of solutes, in particular those with complicated geometry. This demonstration of the role of solvation raises important questions about the driving forces behind biological self-assembly and the paramount role of geometry.

Keywords: geometry; morphometric energy; self-assembly; solvation; tobacco mosaic virus.

Fig. 1.

A) The helical conformation of protein subunits of TMV, using experimentally obtained structural data from the Protein Database with identifier $\text{6R7M}$ (25). B) The intermediate disk aggregate, where 17 protein subunits form a disk structure, using structural data from the Protein Database with identifier $\text{1EI7}$ (26).

Fig. 2.

A) A plot of $F_{\mathrm{sol}}^{*}$ relative to the dissolved state within the simulation. The location of three particular configurations shown in (B–D) are noted. B) Stucture of the noninteracting, dissolved state C) a correctly aligned intermediate state and D) the lowest solvation free energy state close to experimentally observed assembly. E) The evolution of the volume term contribution ($V_i=V(S_i)$) throughout the simulation. F) The evolution of the surface area term ($A_i=A(S_i)$). G) The evolution of the integrated mean curvature term ($C_i=C(S_i)$). H) The evolution of the integrated Gaussian curvature term ($X_i=X(S_i)$). I) the linear overlap penalty, and J) the distance of the simulated states to experimentally observed assembly.

Fig. 3.

An array of low solvation free energy states found in simulations of different variants of TMV protein subunits. A) A state close to correct assembly of the $\text{6R7M}$ variant. B) Two stacked subunits found for $\text{6SAE}$. C) Another local solvation free energy minimum for $\text{6SAE}$. D) A local solvation free energy minimum for $\text{6SAG}$. E) A local solvation free energy minimum for $\text{2TMV}$. F) A local solvation free energy minimum for $\text{1EI7}$. These local solvation free energy minimizing states that are sometimes found in simulation are highly dependent on the chosen variant from the PDB used as the subunit geometry. G) A plot showing the distribution of 100 local minimizers found after HMC refinement for each subunit variant.

Fig. 4.

Two simulation runs using RWM of three TMV protein subunits. A and F) $F_{\mathrm{sol}}^{*}$ (relative to the dissolved state) throughout the simulation run is shown. One can see that the solvation free energy progresses to a minimum. B–E) Four states from the simulation run in (A), as noted on the solvation free energy plot. The final state in (E) is the solvation free energy minimizer, and is comparable to the correct assembly of three subunits in TMV as found consecutively winding up the final helical structure. G–J) Four states from the simulation run in (F), as noted on the solvation free energy plot. The final state in (J) is the solvation free energy minimizer and is comparable to the correct assembly of three subunits in TMV taking the third subunit stacked above the other two, taken around a full turn of the helix.

Fig. 5.

A) $F_{\mathrm{sol}}^{*}$ for a lock and key test geometry, showing how the solvation free energy changes as a unit is moved into a cavity. B) The key structure, colored purple, is inserted into a lock structure, colored yellow, at distance d Å. The yellow molecule is a TMV protein subunit of type $\text{6R7M}$. The purple molecule is an Isoleucin amino acid, with atom centers as residue number 134 of $\text{6R7M}$. The transparent hull represents the parallel surfaces of the atoms inflated by the radius of water. C–F) The remaining sub figures show plots of the weighted measures of the configuration based on the distance between the center of the lock and the key. We have C) weighted volume, D) weighted surface area, E) the weighted integrated mean curvature, and F) the weighted integrated Gaussian curvature.

Fig. 6.

Experimentally determined assemblies of type $\text{6R7M}$ for two (A) and three subunits (B, C).