Single-cell eQTL mapping in yeast reveals a tradeoff between growth and reproduction
- PMID: 40073070
- PMCID: PMC11903034
- DOI: 10.7554/eLife.95566
Single-cell eQTL mapping in yeast reveals a tradeoff between growth and reproduction
Abstract
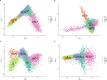
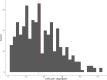
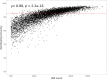
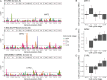
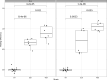
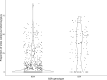
Expression quantitative trait loci (eQTLs) provide a key bridge between noncoding DNA sequence variants and organismal traits. The effects of eQTLs can differ among tissues, cell types, and cellular states, but these differences are obscured by gene expression measurements in bulk populations. We developed a one-pot approach to map eQTLs in Saccharomyces cerevisiae by single-cell RNA sequencing (scRNA-seq) and applied it to over 100,000 single cells from three crosses. We used scRNA-seq data to genotype each cell, measure gene expression, and classify the cells by cell-cycle stage. We mapped thousands of local and distant eQTLs and identified interactions between eQTL effects and cell-cycle stages. We took advantage of single-cell expression information to identify hundreds of genes with allele-specific effects on expression noise. We used cell-cycle stage classification to map 20 loci that influence cell-cycle progression. One of these loci influenced the expression of genes involved in the mating response. We showed that the effects of this locus arise from a common variant (W82R) in the gene GPA1, which encodes a signaling protein that negatively regulates the mating pathway. The 82R allele increases mating efficiency at the cost of slower cell-cycle progression and is associated with a higher rate of outcrossing in nature. Our results provide a more granular picture of the effects of genetic variants on gene expression and downstream traits.
Keywords: S. cerevisiae; eQTL; evolutionary biology; gene expression; genetics; genomics; single-cell RNA sequencing.
© 2024, Boocock et al.
Conflict of interest statement
JB, NA, LA, LW, SP, CM, JB, LK No competing interests declared
Figures

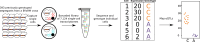









Update of
-
Single-cell eQTL mapping in yeast reveals a tradeoff between growth and reproduction.bioRxiv [Preprint]. 2024 Nov 8:2023.12.07.570640. doi: 10.1101/2023.12.07.570640. bioRxiv. 2024. Update in: Elife. 2025 Mar 12;13:RP95566. doi: 10.7554/eLife.95566. PMID: 38106186 Free PMC article. Updated. Preprint.
References
-
- 10XGenomics VarTrix. 1.0GitHub. 2018 https://github.com/10XGenomics/vartrix
-
- Aguet F, Anand S, Ardlie KG, Gabriel S, Getz GA, Graubert A, Hadley K, Handsaker RE, Huang KH, Kashin S, Li X, MacArthur DG, Meier SR, Nedzel JL, Nguyen DT, Segrè AV, Todres E, Balliu B, Barbeira AN, Battle A, Bonazzola R, Brown A, Brown CD, Castel SE, Conrad DF, Cotter DJ, Cox N, Das S, de Goede OM, Dermitzakis ET, Einson J, Engelhardt BE, Eskin E, Eulalio TY, Ferraro NM, Flynn ED, Fresard L, Gamazon ER, Garrido-Martín D, Gay NR, Gloudemans MJ, Guigó R, Hame AR, He Y, Hoffman PJ, Hormozdiari F, Hou L, Im HK, Jo B, Kasela S, Kellis M, Kim-Hellmuth S, Kwong A, Lappalainen T, Li X, Liang Y, Mangul S, Mohammadi P, Montgomery SB, Muñoz-Aguirre M, Nachun DC, Nobel AB, Oliva M, Park Y, Park Y, Parsana P, Rao AS, Reverter F, Rouhana JM, Sabatti C, Saha A, Stephens M, Stranger BE, Strober BJ, Teran NA, Viñuela A, Wang G, Wen X, Wright F, Wucher V, Zou Y, Ferreira PG, Li G, Melé M, Yeger-Lotem E, Barcus ME, Bradbury D, Krubit T, McLean JA, Qi L, Robinson K, Roche NV, Smith AM, Sobin L, Tabor DE, Undale A, Bridge J, Brigham LE, Foster BA, Gillard BM, Hasz R, Hunter M, Johns C, Johnson M, Karasik E, Kopen G, Leinweber WF, McDonald A, Moser MT, Myer K, Ramsey KD, Roe B, Shad S, Thomas JA, Walters G, Washington M, Wheeler J, Jewell SD, Rohrer DC, Valley DR, Davis DA, Mash DC, Branton PA, Barker LK, Gardiner HM, Mosavel M, Siminoff LA, Flicek P, Haeussler M, Juettemann T, Kent WJ, Lee CM, Powell CC, Rosenbloom KR, Ruffier M, Sheppard D, Taylor K, Trevanion SJ, Zerbino DR, Abell NS, Akey J, Chen L, Demanelis K, Doherty JA, Feinberg AP, Hansen KD, Hickey PF, Jasmine F, Jiang L, Kaul R, Kibriya MG, Li JB, Li Q, Lin S, Linder SE, Pierce BL, Rizzardi LF, Skol AD, Smith KS, Snyder M, Stamatoyannopoulos J, Tang H, Wang M, Carithers LJ, Guan P, Koester SE, Little AR, Moore HM, Nierras CR, Rao AK, Vaught JB, Volpi S, The GTEx Consortium The GTEx Consortium atlas of genetic regulatory effects across human tissues. Science. 2020;369:1318–1330. doi: 10.1126/science.aaz1776. - DOI - PMC - PubMed
-
- Alexa A, Rahnenfuhrer J. Enrichment analysis for gene ontology. Bioconductor; 2022. - DOI
MeSH terms
Associated data
Grants and funding
LinkOut - more resources
Full Text Sources
Other Literature Sources

