Emulating computer models with high-dimensional count output

Abstract

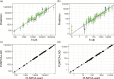
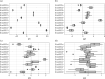
Computer models are used to study the real world, and often contain a large number of uncertain input parameters, produce a large number of outputs, may be expensive to run and need calibrating to real-world observations to be useful for decision-making. Emulators are often used as cheap surrogates for the expensive simulator, trained on a small number of simulations to provide predictions with uncertainty at unseen inputs. In epidemiological applications, for example compartmental or agent-based models for modelling the spread of infectious diseases, the output is usually spatially and temporally indexed, stochastic and consists of counts rather than continuous variables. Here, we consider emulating high-dimensional count output from a complex computer model using a Poisson lognormal PCA (PLNPCA) emulator. We apply the PLNPCA emulator to output fields from a COVID-19 model for England and Wales and compare this to fitting emulators to aggregations of the full output. We show that performance is generally comparable, while the PLNPCA emulator inherits desirable properties, including allowing the full output to be predicted while capturing correlations between outputs, providing high-dimensional samples of counts that are representative of the true model output.This article is part of the theme issue 'Uncertainty quantification for healthcare and biological systems (Part 1)'.

Keywords: Gaussian processes; Poisson lognormal; basis emulation; uncertainty quantification.

Figure 1.

(a) and (b) Predictions for the 50 validation inputs from the PLNPCA-LAD hetGP emulator, aggregated to the overall total (a) and the northeast region (b), plotted against the true simulator output. Points are coloured green if the truth lies within the 95% error bars, blue otherwise. (c) and (d) Comparing mean predictions from the PLNPCA-LAD and PLNPCA-ward hetGP emulators for the overall total (c) and northeast region (d).

Figure 2.

Samples from the PLNPCA-LAD hetGP emulator for nine validation inputs across the 12 LADs in the northeast region. For each, 50 individual samples are plotted in grey, with the mean (solid line) and 95% interval (dashed lines) across 1000 samples in red and true simulator output in black.

Figure 3.

Comparing LAD-level correlations in the training data and from the PLNPCA-LAD emulator. For each region, a single LAD was randomly chosen, and the correlations between this LAD and all 338 others in the training data and emulator samples calculated. In each panel, the LADs are ordered from most to least correlated in the training data.

Figure 4.

Latent coefficients $c_1,c_2,c_3,c_4$ on the PLNPCA-LAD basis for 12 of the ensemble members with 10 replicates. The box plots show the variability in coefficient values across the replicates of these 12 input vectors.

Figure 5.

RMSE between simulator deaths and emulator predictions across the validation set for different sizes of training set ($n=100,150,200$), for samples from the PLNPCA-LAD emulator aggregated to a regional level compared with individually emulating each region. Each point represents a particular split into training and validation sets (50 per $n$).