Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Feb 27;25(5):1451.
doi: 10.3390/s25051451.

Pareto Front Transformation in the Decision-Making Process for Spectral and Energy Efficiency Trade-Off in Massive MIMO Systems

Eni Haxhiraj  1 , Desar Shahu  1 , Elson Agastra  1
Affiliations

Pareto Front Transformation in the Decision-Making Process for Spectral and Energy Efficiency Trade-Off in Massive MIMO Systems

Eni Haxhiraj et al. Sensors (Basel). .

Abstract

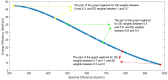
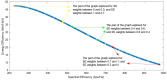
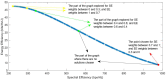
This paper presents a method of choosing a single solution in the Pareto Optimal Front of the multi-objective problem of the spectral and energy efficiency trade-off in Massive MIMO (Multiple Input, Multiple Output) systems. It proposes the transformation of the group of non-dominated alternatives using the Box-Cox transformation with values of λ < 1 so that the graph with a complex shape is transformed into a concave graph. The Box-Cox transformation solves the selection bias shown by the decision-making algorithms in the non-concave part of the Pareto Front. After the transformation, four different MCDM (Multi-Criteria Decision-Making) algorithms were implemented and compared: SAW (Simple Additive Weighting), TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution), PROMITHEE (Preference Ranking Organization Method for Enrichment Evaluations) and VIKOR (Vlse Kriterijumska Optimizacija Kompromisno Resenje). The simulations showed that the best value of the λ parameter is 0, and the MCDM algorithms which explore the Pareto Front completely for different values of weights of the objectives are VIKOR as well as SAW and TOPSIS when they include the Max-Min normalization technique.

Keywords: Box–Cox transformation; decision-making; energy efficiency; optimization; pareto front; spectral efficiency.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflicts of interest in the publication of this article.

Figures

Figure 1
Figure 1
Convex Pareto Front. All Pareto solutions are stable minimum when the coordinate system rotates: 0°, 45°, and 90° [19].
Figure 2
Figure 2
Concave Pareto Front. All Pareto solutions are unstable minimum, except the two points on both ends when the coordinate system rotates: 0°, 45°, and 90° [19].
Figure 3
Figure 3
The shape of the Pareto Front after using the Box–Cox transformation. (a) The original Pareto Front; (b) the Box–Cox transform with λ = 0 (log transform); (c) the Box–Cox transform with λ = 0.5; (d) the Box–Cox transform with λ = −0.5; (e) the Box–Cox transform with λ = −2.
Figure 4
Figure 4
The simulation results for λ = 0: SAW algorithm implemented with Max, Sum and Vector normalization.
Figure 5
Figure 5
The simulation results for λ = 0: SAW algorithm implemented with Max–Min normalization.
Figure 6
Figure 6
The simulation results for λ = 0: TOPSIS algorithm implemented with Max, Sum, and Vector normalization.
Figure 7
Figure 7
The simulation results for λ = 0: TOPSIS algorithm implemented with Max–Min normalization.
Figure 8
Figure 8
The simulation results for λ = 0: PROMITHEE algorithm implemented with V-Shape and Gauss preference function.
Figure 9
Figure 9
The simulation results for λ = 0: VIKOR algorithm.
Figure 10
Figure 10
The simulation results for λ = −0.5: SAW and TOPSIS algorithms implemented with Max, Sum, and Vector normalization.
Figure 11
Figure 11
The simulation results for λ = −0.5: SAW and TOPSIS algorithms implemented with Max–Min normalization.
Figure 12
Figure 12
The simulation results for λ = −0.5: PROMITHEE algorithm implemented with V-Shape preference function.
Figure 13
Figure 13
The simulation results for λ = −0.5: PROMITHEE algorithm implemented with Gauss preference function.
Figure 14
Figure 14
The simulation results for λ = −0.5: VIKOR algorithm.
Figure 15
Figure 15
The simulation results for λ = 0.5: SAW algorithm implemented with Max, Sum, and Vector normalization.
Figure 16
Figure 16
The simulation results for λ = 0.5: SAW algorithm implemented with Max–Min normalization.
Figure 17
Figure 17
The simulation results for λ = 0.5: TOPSIS algorithm implemented with Max, Sum, and Vector normalization.
Figure 18
Figure 18
The simulation results for λ = 0.5: TOPSIS algorithm implemented with Max–Min normalization.
Figure 19
Figure 19
The simulation results for λ = 0.5: PROMITHEE algorithm.
Figure 20
Figure 20
The simulation results for λ =0.5: VIKOR algorithm.
Figure 21
Figure 21
The simulation results for λ = −2: SAW and TOPSIS algorithms implemented with Max, Sum, and Vector normalization.
Figure 22
Figure 22
The simulation results for λ = −2: SAW and TOPSIS algorithms implemented with Max–Min normalization.
Figure 23
Figure 23
The simulation results for λ = −2: PROMITHEE algorithm implemented with V-Shape preference function.
Figure 24
Figure 24
The simulation results for λ = −2: VIKOR algorithm.
See this image and copyright information in PMC

References

    1. Gül B.K., Taşpınar N. Spectral and Energy Efficiency Trade-off in Massive MIMO Systems Using Multi-Objective Bat Algorithm. J. Electr. Eng. 2022;73:132–139. doi: 10.2478/jee-2022-0017. - DOI
    1. Lorincz J., Capone A., Wu J. Greener, Energy-Efficient and Sustainable Networks: State-of-the-Art and New Trends. Sensors. 2019;19:4864. doi: 10.3390/s19224864. - DOI - PMC - PubMed
    1. Lorincz J., Klarin Z. How Trend of Increasing Data Volume Affects the Energy Efficiency of 5G Networks. Sensors. 2022;22:255. doi: 10.3390/s22010255. - DOI - PMC - PubMed
    1. Zhou Y., Zhang O., Xia X., Wei M. Application of MOPSO Algorithm to Optimization of Energy Efficiency and Spectral Efficiency Trade-off in Massive MIMO System; Proceedings of the 2022 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB); Bilbao, Spain. 15–17 June 2022; - DOI
    1. Haxhiraj E., Agastra E., Kamo B. Application of multiobjective evolutionary algorithms for solving the spectral and energy efficiency trade-off problem in Massive MIMO systems: A literature review; Proceedings of the 2nd International Conference on Information Technologies and Educational Engineering (ICITEE); Tirana, Albania. 15–16 December 2023; pp. 95–99.

LinkOut - more resources