The open-closed mod-minimizer algorithm
- PMID: 40098006
- PMCID: PMC11912762
- DOI: 10.1186/s13015-025-00270-0
The open-closed mod-minimizer algorithm
Abstract
Sampling algorithms that deterministically select a subset of -mers are an important building block in bioinformatics applications. For example, they are used to index large textual collections, like DNA, and to compare sequences quickly. In such applications, a sampling algorithm is required to select one -mer out of every window of w consecutive -mers. The folklore and most used scheme is the random minimizer that selects the smallest -mer in the window according to some random order. This scheme is remarkably simple and versatile, and has a density (expected fraction of selected -mers) of . In practice, lower density leads to faster methods and smaller indexes, and it turns out that the random minimizer is not the best one can do. Indeed, some schemes are known to approach optimal density 1/w when , like the recently introduced mod-minimizer (Groot Koerkamp and Pibiri, WABI 2024). In this work, we study methods that achieve low density when . In this small-k regime, a practical method with provably better density than the random minimizer is the miniception (Zheng et al., Bioinformatics 2021). This method can be elegantly described as sampling the smallest closed sycnmer (Edgar, PeerJ 2021) in the window according to some random order. We show that extending the miniception to prefer sampling open syncmers yields much better density. This new method-the open-closed minimizer-offers improved density for small while being as fast to compute as the random minimizer. Compared to methods based on decycling sets, that achieve very low density in the small-k regime, our method has comparable density while being computationally simpler and intuitive. Furthermore, we extend the mod-minimizer to improve density of any scheme that works well for small k to also work well when is large. We hence obtain the open-closed mod-minimizer, a practical method that improves over the mod-minimizer for all k.
Keywords: Hashing; Minimizers; Randomized algorithms; Sketching.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare that they do no have any competing interests.
Figures
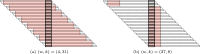




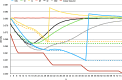


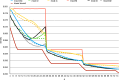

References
-
-
Marchet C, Kerbiriou M, Limasset A. BLight: efficient exact associative structure for
 -mers. Bioinformatics. 2021;37(18):2858–65. 10.1093/bioinformatics/btab217.
-
PubMed
-mers. Bioinformatics. 2021;37(18):2858–65. 10.1093/bioinformatics/btab217.
-
PubMed
-
Marchet C, Kerbiriou M, Limasset A. BLight: efficient exact associative structure for
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous

 -mers. Bioinformatics. 2022;38:185–194. 10.1093/bioinformatics/btac245.
-
-mers. Bioinformatics. 2022;38:185–194. 10.1093/bioinformatics/btac245.
-
 -mer dictionaries. Algorithms Mol Biol. 2023;18(1):1–20. 10.1186/s13015-023-00226-2.
-
-mer dictionaries. Algorithms Mol Biol. 2023;18(1):1–20. 10.1186/s13015-023-00226-2.
-
