Prospective contingency explains behavior and dopamine signals during associative learning
- PMID: 40102680
- PMCID: PMC12148708
- DOI: 10.1038/s41593-025-01915-4
Prospective contingency explains behavior and dopamine signals during associative learning
Abstract
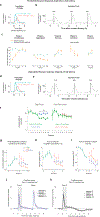
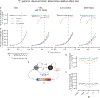
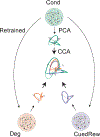
Associative learning depends on contingency, the degree to which a stimulus predicts an outcome. Despite its importance, the neural mechanisms linking contingency to behavior remain elusive. In the present study, we examined the dopamine activity in the ventral striatum-a signal implicated in associative learning-in a Pavlovian contingency degradation task in mice. We show that both anticipatory licking and dopamine responses to a conditioned stimulus decreased when additional rewards were delivered uncued, but remained unchanged if additional rewards were cued. These results conflict with contingency-based accounts using a traditional definition of contingency or a new causal learning model (ANCCR), but can be explained by temporal difference (TD) learning models equipped with an appropriate intertrial interval state representation. Recurrent neural networks trained within a TD framework develop state representations akin to our best 'handcrafted' model. Our findings suggest that the TD error can be a measure that describes both contingency and dopaminergic activity.
© 2025. The Author(s), under exclusive licence to Springer Nature America, Inc.
Conflict of interest statement
Competing interests: The authors declare no competing interests.
Figures




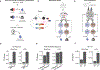






Update of
-
The role of prospective contingency in the control of behavior and dopamine signals during associative learning.bioRxiv [Preprint]. 2024 Feb 6:2024.02.05.578961. doi: 10.1101/2024.02.05.578961. bioRxiv. 2024. Update in: Nat Neurosci. 2025 Jun;28(6):1280-1292. doi: 10.1038/s41593-025-01915-4. PMID: 38370735 Free PMC article. Updated. Preprint.
Similar articles
-
The role of prospective contingency in the control of behavior and dopamine signals during associative learning.bioRxiv [Preprint]. 2024 Feb 6:2024.02.05.578961. doi: 10.1101/2024.02.05.578961. bioRxiv. 2024. Update in: Nat Neurosci. 2025 Jun;28(6):1280-1292. doi: 10.1038/s41593-025-01915-4. PMID: 38370735 Free PMC article. Updated. Preprint.
-
Cue and Reward Evoked Dopamine Activity Is Necessary for Maintaining Learned Pavlovian Associations.J Neurosci. 2021 Jun 9;41(23):5004-5014. doi: 10.1523/JNEUROSCI.2744-20.2021. Epub 2021 Apr 22. J Neurosci. 2021. PMID: 33888609 Free PMC article.
-
Acute Stress Enhances Associative Learning via Dopamine Signaling in the Ventral Lateral Striatum.J Neurosci. 2020 May 27;40(22):4391-4400. doi: 10.1523/JNEUROSCI.3003-19.2020. Epub 2020 Apr 22. J Neurosci. 2020. PMID: 32321745 Free PMC article.
-
Associative and temporal processes: a dual process approach.Behav Processes. 2014 Jan;101:38-48. doi: 10.1016/j.beproc.2013.09.004. Epub 2013 Sep 27. Behav Processes. 2014. PMID: 24076309 Free PMC article. Review.
-
Striatal Dopamine Signals and Reward Learning.Function (Oxf). 2023 Oct 3;4(6):zqad056. doi: 10.1093/function/zqad056. eCollection 2023. Function (Oxf). 2023. PMID: 37841525 Free PMC article. Review.
Cited by
-
The devilish details affecting TDRL models in dopamine research.Trends Cogn Sci. 2025 May;29(5):434-447. doi: 10.1016/j.tics.2025.02.001. Epub 2025 Feb 26. Trends Cogn Sci. 2025. PMID: 40016003 Review.
References
-
- Rescorla RA Pavlovian conditioning. It’s not what you think it is. Am Psychol 43, 151–160 (1988). - PubMed
-
- Hallam SC, Grahame NJ & Miller RR Exploring the edges of Pavlovian contingency space: An assessment of contingency theory and its various metrics. Learning and Motivation 23, 225–249 (1992).
-
- Cheng PW From covariation to causation: A causal power theory. Psychological review 104, 367 (1997).
-
- Gallistel CR, Craig AR & Shahan TA Contingency, contiguity, and causality in conditioning: Applying information theory and Weber’s Law to the assignment of credit problem. Psychol. Rev. 126, 761–773 (2019). - PubMed
Methods-only references
-
- Bäckman CM et al. Characterization of a mouse strain expressing Cre recombinase from the 3’ untranslated region of the dopamine transporter locus. Genesis 44, 383–390 (2006). - PubMed
-
- Sabatini BL The impact of reporter kinetics on the interpretation of data gathered with fluorescent reporters. bioRxiv 834895 (2019) doi: 10.1101/834895. - DOI
Dataset Reference:
-
- Qian L et al. , Code and Data for Qian et al., 2025, Figshare, doi: 10.6084/m9.figshare.28216202, 2025 - DOI
MeSH terms
Substances
Grants and funding
- FA9550-20-1-0413/United States Department of Defense | United States Air Force | AFMC | Air Force Office of Scientific Research (AF Office of Scientific Research)
- U19 NS113201/NS/NINDS NIH HHS/United States
- NARSAD Young Investigator no. 30035/Brain and Behavior Research Foundation (Brain & Behavior Research Foundation)
- R01DC017311/U.S. Department of Health & Human Services | NIH | National Institute on Deafness and Other Communication Disorders (NIDCD)
- 8470652-01/Simons Foundation
LinkOut - more resources
Full Text Sources
Molecular Biology Databases

