Optimal Control of an Electromechanical Energy Harvester

Abstract

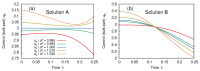
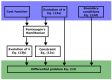
Many techniques originally developed in the context of deterministic control theory have recently been applied to the quest for optimal protocols in stochastic processes. Given a system subject to environmental fluctuations, one may ask what is the best way to change its controllable parameters in time in order to maximize, on average, a certain reward function, while steering the system between two pre-assigned states. In this work, we study the problem of optimal control for a wide class of stochastic systems, inspired by a model of an energy harvester. The stochastic noise in this system is due to the mechanical vibrations, while the reward function is the average power extracted from them. We consider the case in which the electrical resistance of the harvester can be changed in time, and we exploit the tools of control theory to work out optimal solutions in a perturbative regime, close to the stationary state. Our results show that it is possible to design protocols that perform better than any possible solution with constant resistance.

Keywords: energy harvesting; optimal control; stochastic processes.

Figure 2

Characterization of the solutions of PMP. Panels (a,b) show the intensity of the infinite discontinuities $u_0$ and $u_f$ occurring at the beginning and at the end of the protocol in the two physically admissible solutions A and B of system (31). Different choices of the stationary control $u_s$, fixing the boundary conditions (37), are considered. Panels (c,d) account for the corresponding net power gain (or loss) with respect to the stationary strategy $u=u^{*}$. The red squares refer to the value of the average power computed within the perturbative approach. Green circles are obtained by plugging the solution protocol u into the original (non-perturbative) dynamics, and computing the average power of the process (see the caption of Figure 4 for details). Of course, in this case the final state $\sigma \left(t_f\right)$ will not match the prescribed boundary condition exactly—see Figure 4. The distance between the two curves is an indicator of the quality of the perturbative approximation. Finally, the blue triangles represent, for reference, the power obtained with a stationary protocol $u=u_s$. Parameters: $\alpha =0$, $\beta =1$, $\zeta =2$ and $t_f=0.25$.

Figure 3

Bulk part $u_b$ of the protocol, for the two solutions A (a) and B (b), as a function of time. Different boundary conditions are considered. Parameters as in Figure 2.

Figure 4

Dynamics of the system within solution B for boundary conditions fixed by $u_s=1.02u^{*}$. Panels (a–c) show the evolution of the elements of the vector $\sigma$ (the covariances $〈v^2〉$, $〈vI〉$ and $〈I^2〉$), as computed in the perturbative approach (red solid curves). By inserting the solution protocol u, shown in panel (d), back into the original dynamics (33), it is possible to compute the true behavior of the system under the prescribed protocol (computation has been carried out using an explicit Runge–Kutta integration scheme of 4-th order): this evolution is represented by the blue dashed curves in panels (a–c). While it is expected that the two sets of curves do not overlap, the fact that they stay close is a consistency check on our perturbative approximation. Parameters as in Figure 2.

Figure 1

Scheme of the optimal control strategy leading to the differential system Equation (13).