Edge-Centric Embeddings of Digraphs: Properties and Stability Under Sparsification

Abstract

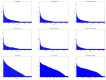
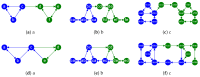
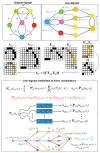
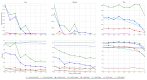
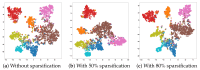
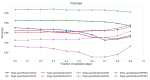
In this paper, we define and characterize the embedding of edges and higher-order entities in directed graphs (digraphs) and relate these embeddings to those of nodes. Our edge-centric approach consists of the following: (a) Embedding line digraphs (or their iterated versions); (b) Exploiting the rank properties of these embeddings to show that edge/path similarity can be posed as a linear combination of node similarities; (c) Solving scalability issues through digraph sparsification; (d) Evaluating the performance of these embeddings for classification and clustering. We commence by identifying the motive behind the need for edge-centric approaches. Then we proceed to introduce all the elements of the approach, and finally, we validate it. Our edge-centric embedding entails a top-down mining of links, instead of inferring them from the similarities of node embeddings. This analysis is key to discovering inter-subgraph links that hold the whole graph connected, i.e., central edges. Using directed graphs (digraphs) allows us to cluster edge-like hubs and authorities. In addition, since directed edges inherit their labels from destination (origin) nodes, their embedding provides a proxy representation for node classification and clustering as well. This representation is obtained by embedding the line digraph of the original one. The line digraph provides nice formal properties with respect to the original graph; in particular, it produces more entropic latent spaces. With these properties at hand, we can relate edge embeddings to node embeddings. The main contribution of this paper is to set and prove the linearity theorem, which poses each element of the transition matrix for an edge embedding as a linear combination of the elements of the transition matrix for the node embedding. As a result, the rank preservation property explains why embedding the line digraph and using the labels of the destination nodes provides better classification and clustering performances than embedding the nodes of the original graph. In other words, we do not only facilitate edge mining but enforce node classification and clustering. However, computing the line digraph is challenging, and a sparsification strategy is implemented for the sake of scalability. Our experimental results show that the line digraph representation of the sparsified input graph is quite stable as we increase the sparsification level, and also that it outperforms the original (node-centric) representation. For the sake of simplicity, our theorem relies on node2vec-like (factorization) embeddings. However, we also include several experiments showing how line digraphs may improve the performance of Graph Neural Networks (GNNs), also following the principle of maximum entropy.

Keywords: digraph sparsification; edge embedding; edge mining; graph neural networks; line digraph; maximum entropy.

Figure 1

The Long-Tail Effect. Histogram of occurrence of each node in the random walks for Cora (top), Citeseer (middle) and Wiki (bottom) datasets, by using the original graph (left), the line graph (center), and the iterated line graph (right). y axis is represented in log scale.

Figure 2

Examples of (a,d) original digraphs, (b,e) their line digraphs, and (c,f) their iterated line digraphs. The color of the nodes represents two different labels. Herein, edges are labeled using the label of the destination node. In other application domains may be more convenient to use the label of the source.

Figure 3

Explanation of the Linearity Theorem. (Top): Input digraph G and its line digraph $\ell G$. Colors index nodes as well as edges destinations. Example: compute ${\mathbf{P}}_{\ell G}^4(e_{10},e_9)$, where $e_{10}$ is a hub and $e_9$ is an authority. (Middle): Adjacencies ${\mathbf{A}}_G$ vs. ${\mathbf{A}}_{\ell G}$. Clearly, $rank\left({\mathbf{A}}_{\ell G}\right)=n$, with $n=6$ nodes in this case. ${\mathbf{E}}_{out}$ retains the n different rows of ${\mathbf{A}}_{\ell G}$. ${\mathbf{E}}_{in}$ is the indicator matrix where ${\mathbf{E}}_{in}(i,j)=1$ means that $e_i$ belongs to the class of equivalence $j=1,\dots ,n$. Then, ${\mathbf{E}}_{out}{\mathbf{E}}_{in}$ is a permutation of ${\mathbf{A}}_G$ (see colors to uncover the permutation matrix $\mathbf{Q}$ making ${\mathbf{A}}_G={\mathbf{Q}}^T{\mathbf{E}}_{out}{\mathbf{E}}_{in}\mathbf{Q}$). (Bottom): Explicit linear combinations. ${\mathbf{P}}_{\ell G}^r$ as a function of ${\mathcal{P}}_G^{r-1}$ (taking $\mathbf{Q}$ into account). ${\mathbf{P}}_{\ell G}^4(e_{10},e_9)$ results from the aggregation of 3 paths in G, all of them starting from $e_{10}^{-}=V_1$ and ending at any node $e_k^{-}\in V$ in 3 steps. Two of the paths reach $V_6=e_{k=6}^{-}$ (and also $V_5=e_{k=9}^{-}$) and another one reachs $V_5=e_{k=9}^{-}$. Since only $e_6$ is linked with $e_9$, we only retain the scores of the paths reaching $V_6=e_{k=6}^{-}$, i.e., ${\mathbf{P}}_{\ell G}^4(e_{10},e_9)={\displaystyle \frac{1}{3}}+{\displaystyle \frac{1}{9}}={\displaystyle \frac{4}{9}}$.

Figure 4

Classification stability. (Top): directed single-label citation networks. Legend: node2vec node refers to performance for the nodal embedding, node2vec edge refers to performance for edge embedding, and similarly for NetFM and HOPE. (Bottom): undirected multi-label networks. (Top): Micro-F1 score. (Bottom): Macro-F1 score.

Figure 5

Clustering stability: Evolution of ARI (top) vs. evolution of modularity (bottom) for different sparsification levels (fraction of preserved edges). Legend: same as in classification results.

Figure 6

Visualization of learned edge embeddings using t-SNE dimensionality reduction of the Cora dataset. Colors represent different ground truth classes. Note that even with significant sparsification (80% of edges removed), the embedding space maintains clear community structures and distinct class boundaries, demonstrating the entropy-preserving properties of line digraphs even under aggressive edge reduction.

Figure 7

Comparison of node and edge sparsification strategies across GNN architectures on the Cora dataset. Solid lines represent node sparsification, dashed lines represent edge sparsification. The x-axis indicates the fraction of edges preserved (from 0.0 to 1.0), while the y-axis shows classification accuracy. Edge sparsification consistently outperforms node sparsification, with GraphSAGE (dashed green) showing remarkable stability even with minimal edge retention.

Figure 8

Comparison of node and edge sparsification strategies across GNN architectures on the Citeseer dataset. Solid lines represent node sparsification, dashed lines represent edge sparsification. The performance gap between edge and node sparsification is more pronounced in Citeseer than in Cora, with edge-based methods (dashed lines) maintaining consistently higher accuracy across all sparsification levels. This suggests that preserving edges is particularly important for maintaining the structural information in citation networks with sparse connectivity patterns.

Figure 9

Comparison of node and edge sparsification strategies across GNN architectures on the Pubmed dataset. Solid lines represent node sparsification, dashed lines represent edge sparsification. All GNN architectures show remarkable stability under edge sparsification (dashed lines), with GraphSAGE maintaining above 90% accuracy even with only 10% of edges preserved. This demonstrates that strategic edge preservation captures the essential topology of the graph, aligning with our theoretical findings about the maximal entropy properties of line digraphs.