Nanoscale engineering and dynamic stabilization of mesoscopic spin textures

Abstract

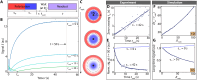
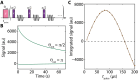
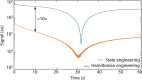
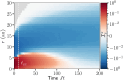
Thermalization, while ubiquitous in physics, has traditionally been viewed as an obstacle to be mitigated. In contrast, we demonstrate here the use of thermalization in the generation, control, and readout of "shell-like" spin textures with interacting ¹³C nuclear spins in diamond, wherein spins are polarized oppositely on either side of a critical radius. The textures span several nanometers and encompass many hundred spins; they are created and interrogated without manipulating the nuclear spins individually. Long-time stabilization is achieved via prethermalization to a Floquet-engineered Hamiltonian under the electronic gradient field: The texture is therefore metastable and robust against spin diffusion. This enables the state to endure over multiple minutes before it decays. Our work on spin-state engineering paves the way for applications in quantum simulation and nanoscale imaging.

Fig. 1.. System and readout.

(A) Spin textures. Controllable “shell-like” spin texture of positive and negative polarization (shaded red and blue, respectively) is generated in a nanoscale ensemble of ¹³C nuclear spins surrounding a central NV electron (manipulated by an external laser, shown in green). The domains are separated by the critical radius r_c at the domain boundary (dashed white line). The texture encompasses $\sim \mathcal{O}\left(100\right)$ spins within the critical radius and remains stable for minutes. The optically pumped electron serves as a spin injector and produces a nanoscale magnetic field gradient B (shaded light pink) that stabilizes the spin texture in a prethermal state. (B) Experimental schematic showing prethermalization caused by periodic driving at high-magnetic field (HF) B₀ ≥ 7 T, with a train of spin-locking θ-pulses of length t_p. $\widehat{\mathbf{x}}-\widehat{\mathbf{y}}$ spin polarization is interrogated in windows between the pulses for total readout times t > 60 s (>0.5M pulses). au, arbitrary units. (C) ¹³C spin texture is generated and stabilized by a spatially varying potential φ(r) created upon driving with θ ≈ π in the presence of the NV gradient (compare the “Robust spin shells by Hamiltonian engineering” section).

Fig. 2.. Spin textures via hyperpolarization injection (state engineering).

(A) Net ¹³C spin polarization under positive (τ₊, red points), followed by negative τ₊ = 60 s (τ₋, blue points) hyperpolarization injection at room temperature. Solid lines represent a biexponential fit. The t_pol ≈ 97 s box corresponds to ≈0 net polarization. (B) Normalized spin-lock decays under periodic drive with θ ≈ π/2, showing (i) signal 𝑆 and (ii) rotating-frame phase ϕ_R. Dashed black line: spin-lock decay corresponding to τ₋ = 0 [a in (A)], displaying long lifetimes $T{\prime }_2\approx 93.4$ s. Colored lines: data for different τ₋ values. Decay profiles for the τ₋ inset from (A) exhibit a sharp zero crossing at t = t_zc (II) and associated phase inversion (see ii). Dark orange line: τ₋ = 44.8 s emphasized for clarity. The full dataset is shown in movie S1. (iii) Zero-crossing t_zc movement with τ₋ demonstrates control of spin texture. (C) Schematic representation of spin textures with increasing experiment progression time 𝑡. Representative points (I to IV) are marked on τ₋ = 44.8 s in (B). NV is at r = 0. Positive (negative) polarization is shaded red (blue). Electron-driven dissipation decreases polarization (white) around r = 0. Growing texture size and increasing white region at the +/− boundary indicate spin diffusion; the dashed line represents the polarization regime. (D) (i) Fourier-transformed ¹³C NMR spectrum of full τ₋ = 30-, 34-, and 37-s data in (B). (ii) FT data for varying τ₋ are plotted on a logarithmic scale comprising 91 τ₋ slices, separated by 0.2 s with a >109 variation in intensity. Spectral narrowing with increasing τ₋ indicates that fast-relaxing ¹³C nuclear spins near the NV are first depolarized until inversion of the total signal with τ₋ ≈ 37 s [boxed region in (A)].

Fig. 3.. Melting of spin texture because of spin diffusion (state engineering).

(A) Experiment schematic. Waiting period 𝑡_wait at a high field is introduced after successive {τ₊, τ₋} spin injection and before application of the periodic drive in Fig. 2. (B) Representative signal traces showing changes in decay profiles with variable 𝑡_wait for texture generated with τ₊ = 60 s and τ₋ = 42 s (bolded trace in Fig. 2B). The decrease in signal amplitude between t_wait = 0 and t_wait = 30 s evidences the instability of state-engineered spin texture. A full movie of this dataset, with phase information can be found in movie S2. (C) Schematic representation showing the melting of spin texture during t_wait because of spin diffusion at the boundary between polarization layers. The dashed line serves as a guide to the eye for the domain wall boundary. (D) Points show the movement of the zero-crossing t_zc position with t_wait for data in (B). The solid line is a linear fit. (E) Signal intensity at t = 50 s in (B) plotted for different values of t_wait normalized to its value corresponding to the t_wait = 0 case. Melting of the spin texture because of diffusion manifests as a decrease in signal. The solid line is a biexponential fit. The light blue line corresponds to the case without spin texture (τ₊ = 60 s, τ₋ = 0). (F and G) Simulations corresponding to (D) and (E) showing zero-crossing times and |min(${\mathcal{I}}_x$)| extracted from numerical time evolution in a 1D short-range model using a similar shell-like initial state (see Fig. 5 and Materials and Methods). Simulations show qualitative agreement with experimental results.

Fig. 4.. Robust spin textures by Hamiltonian engineering.

(A) Experiment schematic. Spins are hyperpolarized for τ₊ = 90 s and subject to a spin-locking train with θ ≈ π. (B) The measured signal S undergoes sharp zero crossing and associated sign inversion [the phase signal is analogous to Fig. 2B(ii) and not shown]. Colored lines show variation with θ (see the color bar). Each trace has ≈0.5M points. The dark purple trace highlights representative data at θ/π = 0.94 for clarity, with sharp zero crossing at time t_zc. (C) Analogous signal to the bolded purple trace in (B), with small frequency offset (see section S6). The signal is plotted on a logarithmic scale and extends for t > 150 s. Marked signal zero crossing is evident. (D) Schematic representation of formed spin texture for key points of the bolded trace in (B) (marked I to IV). Signal zero crossing arises because of thermalization to an effective Hamiltonian ${\mathcal{H}}_{\text{eff}}$ bearing spatial texture arising from the NV-imposed gradient (Fig. 1C). The dashed black line indicates the domain boundary at r_c. The spin texture remains robust against spin diffusion with t (see Fig. 5A). (E) Movement of zero crossing with θ. 2D color plot showing logarithmic scale visualization of data in (B) plotted with respect to θ (horizontal slices). Zero crossing appears as an abrupt decrease in signal (colored blue). The θ = π slice is marked and corresponds to a rapid signal decay. t_zc occurs at later times for smaller θ. Point III corresponding to zero crossing in (B) is marked. (F) Numerical simulations performed with LITE for the simplified short-range model with the experimental data (see Fig. 5 and section S9).

Fig. 5.. Simulations of spin texture formation and evolution using the effective model Hamiltonians for state engineering and Hamiltonian engineering.

Panels (A) and (B) are obtained from 1D short-range simulations for infinitely extended systems including effects of dissipation using the LITE algorithm (see section S9A). The system extends in both directions, but only positive values are shown. The horizontal axis displays interrogation time t in J⁻¹ units, and the vertical axis displays distance r from NV in arbitrary units. (A) Spin texture via state engineering. We imprint the spin texture in the initial state using 11 positively polarized spins close to the NV center at r = 0 followed by 18 negatively polarized spins. (i) Colors display polarization ${\mathcal{I}}_r^x\left(t\right)$ (color bar) at different sites at time t (vertical slices). The panel displays spreading dynamics with t. Formed shells melt under diffusion (see section S9C). (ii) Integrated polarization over the spin ensemble, corresponding to signal 𝑆 measured in Fig. 2. Simulations reveal formation of a sharp zero crossing in either case (t_zc marked), occurring at the instance of zero total net polarization. (B) Spin texture via Hamiltonian engineering. The initial state at t = 0 contains 11 positively polarized spins within a background of spins in a fully mixed state. (i) Polarization ${\mathcal{I}}_r^x\left(t\right)$ (color bar) showing that spin texture forms via thermalization. Late-time behavior (dashed line) follows energy diffusion $\propto \sqrt{t}$. The shell critical radius r_c (horizontal dashed line) is stabilized. (ii) Integrated ensemble polarization showing formation of zero crossing analogous to Fig. 4. (C and D) Formed shells in three dimensions via Hamiltonian engineering, obtained from late-time dynamics of classical 3D long-range simulations (see fig. S29 for full-time traces). For the classical simulation, dissipation is not considered and spins within the frozen core [white region in (D)] are not simulated.

Fig. 6.. Novel instrumentation for cryogenic DNP.

(A) Device construction. CAD model showing instrument and highlighting main components. It consists of a 9.4-T superconducting magnet, surrounded by an aluminum frame to which a 4-K cryostat is mounted on a belt-driven actuator, bearing a high-torque motor. A laser illuminates the sample from the bottom. (B) Photograph showing key features of the instrument. The cryostat is shown at the low-field position B_pol; the actuator truck and mounts are visible. 2 in, 5.08 cm. (C) CAD model showing the schematic of the NMR/DNP probe. It fits snugly within the cryostat, providing additional rf shielding. Tuning rods [>3 ft. (>91.44 cm) long] extend through the top of the probe and allow for rf cavity tuning and impedance matching, even under vacuum and cryogenic conditions. 4 in, 10.16 cm. (D) Photograph of the constructed probe. A close-up of coil arrangement is shown, highlighting the rf saddle coil and centrally placed MW loop used for hyperpolarization. The aperture at the probe base enables optical access to the sample. 1 in, 2.54 cm.

Fig. 7.. Estimation of flip angle θ.

(A) Schematic of spin-locking Rabi experiment, consisting of a train of π/2 pulses, where the angle of the first pulse θ_init is varied. (B) Typical signals in case of θ_init = π/2 and θ_init = π, with total measurement time of t = 70 s, corresponding to >0.5M pulses. (C) Variation of integrated signal S_int with the length of the first pulse. The solid line represents sinusoidal fit. Slight off-resonance in the pulses leads to a finite signal even at θ_init = 0.

Fig. 8.. Comparison of state and Hamiltonian engineering signals.

Comparison of signal S for state engineering data in Fig. 2 (taken at room temperature) and Hamiltonian engineering data from Fig. 4 (taken at 100 K) for comparable zero-crossing times t_zc ≈ 31 s. Data are shown on a logarithmic scale for clarity. The measured signal is over an order of magnitude greater in the Hamiltonian engineering method.

Fig. 9.. Zero-crossing radius for state engineering.

Zoom-in to the Jt < 200 region in Fig. 5A(i) with an adjusted color map scale to reveal polarization dynamics close to NV (r = 0). The dynamics of positive polarization close to NV are dominated by dissipation such that it decays to zero before the crossing radius can move outward because of diffusion.

Fig. 10.. Waiting time simulations.

(A) Time-evolution curves of the total $\widehat{\mathbf{x}}$-polarization for different waiting times. After t_wait, the dissipation acting on the site with r = r_NV is switched on. For increased waiting time, the corresponding zero-crossing time increases since polarization spreads diffusively during t_wait, diminishing the effect of dissipation, which acts most strongly at the position of the NV (r_NV = 0). We use an initial domain wall state with a total of N₊ + N₋ = 31 initially polarized spins where the N₊ = 13 [panel (i), blue] and N₊ = 11 [panel (ii), orange] spins closest to r_NV have p_r = 0.6 and the remaining N₋ = 31 − N₊ spins have p_r = −0.2 (here, ${\mathrm{\rho }}_n\propto 1+p_r{I}_r^x$). The dissipation parameters are ${\mathrm{\gamma }}_z={\mathrm{\gamma }}_{+}={\mathrm{\gamma }}_{-}=0.5J$ and the other simulation parameters as in fig. S16. (B) Zero-crossing time t_zc of the curves in (A) measured from t_wait as a function of t_wait. (C) Absolute value of the minimum attained value of the total $\widehat{\mathbf{x}}$-polarization of the curves in (A) as a function of the waiting time, normalized with respect to t_wait = 0. In addition to the domain wall initial states, we also perform a simulation with a uniformly polarized initial state with N₋ = 0 (N₊ = 31) [red curve, (iii)].