Strong Coupling Møller-Plesset Perturbation Theory
- PMID: 40163020
- PMCID: PMC12020365
- DOI: 10.1021/acs.jctc.5c00055
Strong Coupling Møller-Plesset Perturbation Theory
Abstract
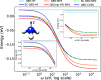
Perturbative approaches are methods to efficiently tackle many-body problems, offering both intuitive insights and analysis of correlation effects. However, their application to systems where light and matter are strongly coupled is nontrivial. Specifically, the definition of suitable orbitals for the zeroth-order Hamiltonian represents a significant theoretical challenge. While reviewing previously investigated orbital choices, this work presents an alternative polaritonic orbital basis suitable for the strong coupling regime. We develop a quantum electrodynamical (QED) Møller-Plesset perturbation theory using orbitals obtained from the strong coupling QED Hartree-Fock. We assess the strengths and limitations of the different approaches with emphasis on frequency and coupling strength dispersions, intermolecular interactions and polarization orientational effects. The results show the essential role of using a consistent molecular orbital framework in order to achieve an accurate description of cavity-induced electron-photon correlation effects.
Conflict of interest statement
The authors declare no competing financial interest.
Figures


 . When the polarization has a component
along the displacement direction the QED-MP2 method displays an unphysical
behavior in the long-range regime.
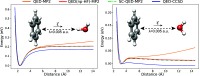
. When the polarization has a component
along the displacement direction the QED-MP2 method displays an unphysical
behavior in the long-range regime.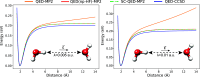


References
-
- Flick J.; Rivera N.; Narang P. Strong light-matter coupling in quantum chemistry and quantum photonics. Nanophotonics 2018, 7, 1479–1501. 10.1515/nanoph-2018-0067. - DOI
LinkOut - more resources
Full Text Sources
