Analysis of the spatio-temporal dynamics of a Rho-GEF-H1-myosin activator-inhibitor reaction-diffusion system

Abstract

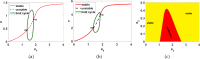
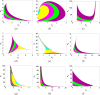
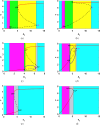
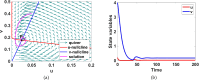
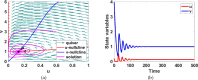
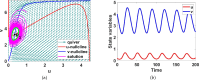
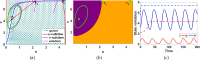
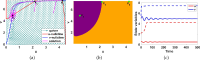
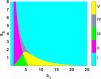
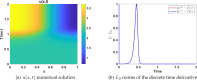
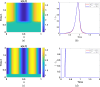
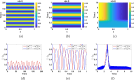
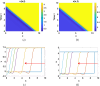
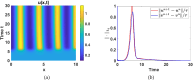
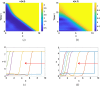
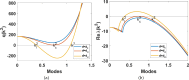
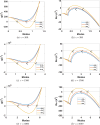
This study presents a detailed mathematical analysis of the spatio-temporal dynamics of the RhoA-GEF-H1-myosin signalling network, modelled as a coupled system of reaction-diffusion equations. By employing conservation laws and the quasi-steady state approximation, the dynamics is reduced to a tractable nonlinear system. First, we analyse the temporal system of ordinary differential equations (ODE) in the absence of spatial variation, characterizing stability, bifurcations and oscillatory behaviour through phase-plane analysis and bifurcation theory. As parameter values change, the temporal system transitions between stable dynamics; unstable steady states characterized by oscillatory dynamics; and co-existence between locally stable steady states, or co-existence between a locally stable steady state and a locally stable limit cycle. Second, we extend the analysis to the reaction-diffusion system by incorporating diffusion to the temporal ODE model, leading to a comprehensive study of Turing instabilities and spatial pattern formation. In particular, by adding appropriate diffusion to the temporal model: (i) the uniform steady state can be destabilized leading to the well-known Turing diffusion-driven instability (DDI); (ii) one of the uniform stable steady states in the bistable region can be driven unstable, while the other one remains stable, leading to the formation of travelling wave fronts; and (iii) a stable limit cycle can undergo DDI leading to the formation of spatial patterns. More importantly, the interplay between bistability and diffusion shows how travelling wavefronts can emerge, consistent with experimental observations of cellular contractility pulses. Theoretical results are supported by numerical simulations, providing key insights into the parameter spaces that govern pattern transitions and diffusion-driven instabilities.

Keywords: Rho-GEF-Myosin signalling network; Turing diffusion-driven instability; activator-inhibitor system; bifurcation analysis; reaction-diffusion; travelling wave front.

Figure 1.

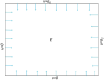
A schematic representation of the experimental model for the Rho-GEF-myosin signalling network from which mathematical equations are derived [21]. In this visual representation, the symbols $G_a$ , $R_a$ and $M_a$ denote the active states of GEF, Rho and myosin, while $G_i$ , $R_i$ and $M_i$ signify their respective inactive states. Reaction rates are represented as $k_1$ , $k_2$ , $k_3$ , $k_4$ , $k_5$ and $k_6$ , and the Michaelis–Menten constants are denoted as $K_{m_1}$ , $K_{m_2}$ , $K_{m_3}$ and $K_{m_4}$ . The broken red lines represent a positive feedback loop while blue lines represent a negative feedback loop.

Figure 2.

Numerical bifurcation results corresponding to system (2.3) with set 1 parameter values as listed in table 6. Plots (a) and (b) represent one-parameter bifurcation diagrams with bifurcation parameter $a_1$ . HB stands for the Hopf bifurcation point, and the dashed black line represents the values of $u$ and $v$ in the unstable region, while the solid red line represents the values of $u$ and $v$ in the stable region. Hopf bifurcation points occur at $a_1=1.365$ and $a_1=1.839$ . The green loop indicates the upper and lower limits of the resultant limit cycle. (c) represents the two-parameter bifurcation diagram with bifurcation parameters $a_1$ and $a_5$ . The red region represents the oscillatory region, while the lime region represents the stable region.

Figure 3.

Numerical simulations showing temporal evolution profiles of $u(t)$ and $v(t)$ corresponding to system (2.3), with set 1 parameter values as listed in table 6 with (a) $a_1=0.5$ . (b) $a_1=1.5$ . (c) $a_1=2$ .

Figure 4.

Turing instability regions in selected pairwise parameter planes for different $d$ values. All other parameters remain fixed, as indicated in table 6. The explanation of the regions is shown in table 4.

Figure 5.

One parameter bifurcation diagrams corresponding to (a) $u^{*}$ against $a_1$ for $a_5=0.5$ , (b) $v^{*}$ against $a_1$ for $a_5=0.5$ , (c) $u^{*}$ against $v$ for $a_5=\mathrm{1,5}$ , (d) $v^{*}$ against $a_1$ for $a_5=1.5$ and (e) $u^{*}$ against $a_1$ for $a_1=2$ (f) $v^{*}$ against $a_1$ for $a_5=2$ . In all diagrams, LP and HB represent fold and Hopf bifurcation points, respectively.

Figure 6.

(a) Phase plane diagram showing that the uniform steady state ${\displaystyle {\mathit{P}}_{\mathbf{1}}}$ is globally asymptotically stable and, (b) the $u(t)$ and $v(t)$ time evolution for system (2.3) corresponding to region I of figure 11 . Here $a_1=0.2$ and $a_5=2$ .

Figure 7.

(a) Phase plane diagram showing that the uniform steady state ${\displaystyle {\mathit{P}}_{\mathbf{2}}}$ is globally asymptotically stable and, (b) the $u(t)$ and $v(t)$ time evolution for system (2.3) corresponding to region II shown in figure 11, Here $a_1=2$ and $a_5=1$ .

Figure 8.

(a) Phase plane diagram showing the limit cycle around the uniform steady state ${\displaystyle {\mathit{P}}_{\mathbf{3}}}$ , coloured green. (b) $u(t)$ and $v(t)$ time evolution for system (2.3) corresponding to region III of figure 11. Here $a_1=4$ and $a_5=1.5$ .

Figure 9.

(a) Phase plane diagram showing coexistence of a L.A.S limit cycle (green loop) and L.A.S uniform steady state, ${\displaystyle {\mathit{P}}_{\mathbf{9}}}$ , (b) the basin of attraction for the limit cycle around the uniform steady state ${\displaystyle {\mathit{P}}_{\mathbf{7}}}$ and the steady state ${\displaystyle {\mathit{P}}_{\mathbf{9}}}$ , and (c) the $u(t)$ and $v(t)$ time evolution for system (2.3) corresponding to region V of figure 11. Here $a_1=5$ and $a_5=1.5$ together with initial conditions $(0.61,3.1)$ and $(2.1,5.5)$ .

Figure 10.

(a) Phase plane diagram showing coexistence of three uniform steady states, ${\displaystyle {\mathit{P}}_{\mathbf{4}}}$ , ${\displaystyle {\mathit{P}}_{\mathbf{5}}}$ and ${\displaystyle {\mathit{P}}_{\mathbf{6}}}$ , (b) the basin of attraction for the uniform steady states ${\mathbf{P}}_{\mathbf{4}}$ and ${\mathbf{P}}_{\mathbf{6}}$ , and (c) the $u(t)$ and $v(t)$ time evolution for system (2.3) corresponding to region IV, shown in figure 11. Here $a_1=4.3$ and $a_5=2.1$ . The initial conditions for bistability are (0.6, 5) and (2.1, 5.5).

Figure 11.

Two-parameter numerical bifurcation analysis results corresponding to system (2.3) with $a_1$ and $a_5$ as bifurcation parameters and set 2 parameter values as listed in table 6. I, single non-Turing uniform steady state; II, single Turing-type uniform steady state; III, single unstable uniform steady state; IV, three uniform steady states with one stable and the other unstable (bistable region); V, three uniform steady states with two unstable and one stable.

Figure 12.

Plots of: (a) $u(x,t)$ , and (b) $v(x,t)$ numerical solutions, and (c) the $L_2$ -norm of the discrete time-derivative of $u(x,t)$ and $v(x,t)$ at different time points. Parameters are chosen from region I while the rest are as listed in table 6 with $d=10$ and $\gamma =500$ .

Figure 13.

Plot of: (a) the contours of $u(x,t)$ numerical solutions and (b) the $L_2$ norms of the discrete time-derivatives of $u(x,t)$ and $v(x,t)$ . The parameter values are chosen from region II while the rest are listed in table 6 with $d=10$ and $\gamma =500$ . The numerical solutions qualitatively mirror the profile of the eigenfunction.

Figure 14.

Numerical simulation results corresponding to system (2.1) with parameter values in region II, d = 10 and varying γ.(a) $u(x,t)$ , numerical solution and (b) the $L_2$ norms of the discrete time-derivative of $u(x,t)$ and $v(x,t)$ , with $\gamma =1000$ , while (c) and (d) are respectively the contour plot of $u(x,t)$ and the $L_2$ norms of the discrete time-derivative of $u(x,t)$ and $v(x,t)$ , when $\gamma =5000$ . The profiles of numerical solutions qualitatively reproduce the profiles of the eigenfunctions as predicted by the linear stability theory.

Figure 15.

Numerical simulation results corresponding to system (2.1) with parameter values in region III and d = 50.(a)–(c) Contour plots of $u(x,t)$ for $\gamma =1$ , $\gamma =100$ and $\gamma =250$ respectively, and (d)–(e) the respective $L_2$ -norm of the discrete time-derivative of $u(x,t)$ and $v(x,t)$ .

Figure 16.

Plots of (a) the period and (b) amplitude, against $\gamma$ respectively, corresponding to the limit cycle in region III, with $d=50$ .

Figure 17.

Plots of: (a) $u(x,t)$ , and (b) $v(x,t)$ solutions exhibiting travelling wave fronts and spatial profiles of (c) $u(x,t)$ and (d) $v(x,t)$ at different time points. Parameters are chosen from region IV while the rest are listed in table 6 together with $d=50$ and $\gamma =200$ .

Figure 18.

Plots of: (a) contour plot of $u(x,t)$ , exhibiting the formation of spatially inhomogeneous patterns. (b) Plot of the $L_2$ -norm of the discrete time derivatives of $u(x,t)$ and $v(x,t)$ . Parameters are chosen from region IV while the rest are listed in table 6 together with $d=50$ , $\gamma =200$ and $L=10$ .

Figure 19.

Plots of: (a) $u(x,t)$ , and (b) $v(x,t)$ solutions exhibiting travelling wave fronts. (c) –(d) Snapshots of the spatial profiles of $u(x,t)$ and $v(x,t)$ at different time points. Parameters are chosen from region V while the rest are listed in table 6 together with $d=50$ , $\gamma =200$ .

Figure 20.

A schematic representation showing the flow of solutions when approaching the boundaries of the invariant set $E$ .

Figure 21.

Plots illustrating the interval $k_l^2<k^2<k_r^2$ in which (a) $q(k^2)<0$ and (b) Re $\lambda (k^2)>0$ hold for $d<d_c$ , $d=d_c$ , and $d>d_c$ . Here, $d_c=5.84$ , $\gamma =200$ , $a_7=16$ , in addition to the other parameters from set 2 as listed in table 6.

Figure 22.

Plots for $q(k^2)$ and Re $\lambda (k^2)$ showing the excited modes between $k_l^2$ and $k_r^2$ . (a) – (b): one excited mode, with $\gamma =200$ . (c) –(d): one excited mode, $\gamma =1500$ . (e) – (f): three excited modes, $\gamma =5000$ . See table 7 for the summary of excited modes.