Modeling of mold inactivation via cold atmospheric plasma (CAP)

Abstract

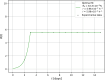
During their reproduction cycles, the omnipresent pathogens produce a broad class of mycotoxins responsible for serious health problems in living organisms. To reduce (or even to eradicate) the microorganisms from the invaded system, various conventional methods are applied in practice, sometimes with counterproductive effects. To overcome these challenges, the cold atmospheric plasma (CAP) is applied to terminate mold proliferation within the system. The paper presents a mathematical model for the elimination of microscopic filamentous types of fungi, specifically molds, by using the CAP. The evolution of mold population is described by a nonlinear logistic equation with a density-dependent inactivation rate. Exactly calculated growth curves are compared with experimental data for Aspergillus brasiliensis obtained for two plasma operating times. The results show that if the plasma inactivation rate is comparable to the maximum natural growth rate of the mycelium, the mold colony becomes extinct after a finite time. Otherwise, the mycelium may survive the plasma intervention. The model presented in the paper can be applied to other classes of microorganisms (e.g., bacteria and viruses), using different inactivation techniques (e.g., heating or high pressures with properly defined inactivation rates).

Importance: The novelty of this study is to model the extinction process of molds from an invaded system by using a nonlinear logistic equation with a density-dependent inactivation rate. The resulting analytical solution allows us to determine the coverage of the surface by mycelium at arbitrary times. The calculated growth curves are compared with data sets for Aspergillus brasiliensis. An advantage of this model is the possibility to obtain relevant information in a matter of minutes, compared to the highly time-consuming real experiments that can take weeks.

Keywords: Aspergillus brasiliensis; cold atmospheric plasma; comparison with experiments; growth curves; mathematical modeling; mycelium inactivation.

Fig 1

Mold detection on melt extract agar (no plasma treatment).

Fig 2

A. brasiliensis on melt extract agar treated with diffuse coplanar barrier discharge.

Fig 3

Growth curve of A. brasiliensis after plasma intervention at t₀=72 h after inoculation.

Fig 4

Modeling of the growth curve of A. brasiliensis with plasma activated at 117 h after inoculation.