Visual outdoor space perception
- PMID: 40185914
- PMCID: PMC11971258
- DOI: 10.1038/s41598-025-96424-6
Visual outdoor space perception
Abstract
Visual space perception has been a topic of sustained research since the nineteenth century. Much of this research into the geometry of visual space, however, required observers to make judgments about spatial relationships between isolated points in total darkness. While a sizeable number of previous investigations have now explored visual space perception in outdoor natural environments, nearly all of the previous investigations evaluating the curvature of visual space have utilized only small numbers of observers. In the current experiment, a large number (30) of observers adjusted triangular configurations of markers in an outdoor field until they appeared either as equilateral or right triangles in depth. There was a wide range of outcomes, such that the observers' judgments were consistent with elliptic, Euclidean, and hyperbolic geometry. There is thus no single consistent relationship between physical space and perceived space. Furthermore, the geometry of visual space frequently changes as the size of spatial configurations is varied-for many observers, judgments for small configurations are consistent with elliptic or Euclidean geometry while judgments for large configurations are frequently consistent with hyperbolic geometry.
© 2025. The Author(s).
Conflict of interest statement
Declarations. Competing interests: The authors declare no competing interests.
Figures
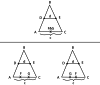



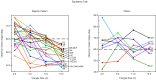

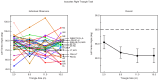
References
-
- Blank, A. A. Analysis of experiments in binocular space perception. J. Opt. Soc. Am.48, 911–925 (1958). - PubMed
-
- Blank, A. A. Curvature of binocular visual space. An experiment. J. Opt. Soc. Am.51, 335–339 (1961).
-
- Koenderink, J. J., van Doorn, A. J. & Lappin, J. S. Direct measurement of the curvature of visual space. Perception29, 69–79 (2000). - PubMed
-
- Battro, A. M., Netto, S. P. & Rozestraten, R. J. A. Riemannian geometries of variable curvature in visual space: Visual alleys, horopters, and triangles in big open fields. Perception5, 9–23 (1976). - PubMed
-
- Norman, J. F., Crabtree, C. E., Clayton, A. M. & Norman, H. F. The perception of distances and spatial relationships in natural outdoor environments. Perception34, 1315–1324 (2005). - PubMed
LinkOut - more resources
Full Text Sources

