Dynamic Response of Concentrated Electrolytes to Chirp Signals
- PMID: 40189843
- PMCID: PMC12004923
- DOI: 10.1021/acsnano.4c14099
Dynamic Response of Concentrated Electrolytes to Chirp Signals
Abstract
Electrolytes, chirp signals, Brownian dynamics, conductivity, Maxwell-Wagner relaxation This study investigates the dynamic response of electrolyte/macroion solutions to time-varying electric fields, which is vital for applications from water desalination to neuromorphic computing and sensor technologies. Using large-scale Brownian dynamics simulations coupled with Poisson's equation, we examined the frequency-dependent conductivity of symmetric and binary electrolytes/nanoparticles across various concentrations. We reveal a comprehensive picture of charge transport mechanisms by employing chirp signals that excite multiple frequencies. Our results identify three distinct dynamic regimes: (1) instantaneous response at low frequencies, (2) increased lagging and imaginary conductivity at intermediate frequencies, and (3) diminished conductivity at high frequencies due to short-time ion/macroion dynamics. Significant deviations from ideal behavior at low frequencies and high concentrations are attributed to packing and many-body interactions. We propose a modified Maxwell-Wagner relaxation time that incorporates excluded volume effects, offering a more accurate time scale for the dynamic response of concentrated electrolytes/macroions. This new framework scales the frequency-dependent conductivity, revealing universal responses across different concentrations and interaction strengths.
Keywords: charged nanoparticles; concentrated electrolytes; conductivity spectra; electrohydrodynamics; nonequilibrium transport.
Conflict of interest statement
The authors declare no competing financial interest.
Figures
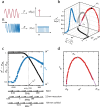
 , where ϕm is the maximum
packing fraction. (c) Increment of the conductivity. The lowest value
for the coupling parameter, ε = 0.5, is shown by blue circle
markers, ε = 2.0 for orange square markers, and ε = 5.0
for green triangle markers.
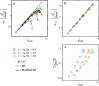
, where ϕm is the maximum
packing fraction. (c) Increment of the conductivity. The lowest value
for the coupling parameter, ε = 0.5, is shown by blue circle
markers, ε = 2.0 for orange square markers, and ε = 5.0
for green triangle markers.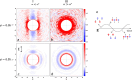

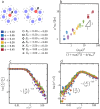
 . (c) Imaginary contribution to the frequency-dependent
conductivity as a function of the rescaled frequency. At frequencies
below ω/ω*, σ″ ∼ ω/ω*
and at frequencies above ω/ω*, σ″ decays
as
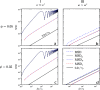
. (c) Imaginary contribution to the frequency-dependent
conductivity as a function of the rescaled frequency. At frequencies
below ω/ω*, σ″ ∼ ω/ω*
and at frequencies above ω/ω*, σ″ decays
as  .
.References
-
- Chen L.; Yin Z.; Li F.; Chen Z. Treatment of Simulated Saline Brine Water by Membrane Distillation Process Enhanced Through Alternating Current Electric Field. Chem. Eng. Res. Des. 2023, 192, 167–179. 10.1016/j.cherd.2023.02.035. - DOI
-
- Noy A.; Li Z.; Darling S. B. Fluid Learning: Mimicking Brain Computing with Neuromorphic Nanofluidic Devices. Nano Today 2023, 53, 102043.10.1016/j.nantod.2023.102043. - DOI
LinkOut - more resources
Full Text Sources

