Online Bayesian changepoint detection for network Poisson processes with community structure
- PMID: 40190469
- PMCID: PMC11968509
- DOI: 10.1007/s11222-025-10606-w
Online Bayesian changepoint detection for network Poisson processes with community structure
Abstract
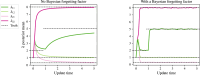
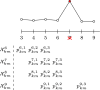
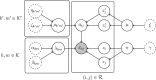
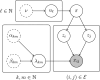
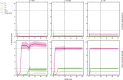
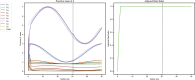
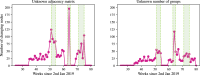
Network point processes often exhibit latent structure that govern the behaviour of the sub-processes. It is not always reasonable to assume that this latent structure is static, and detecting when and how this driving structure changes is often of interest. In this paper, we introduce a novel online methodology for detecting changes within the latent structure of a network point process. We focus on block-homogeneous Poisson processes, where latent node memberships determine the rates of the edge processes. We propose a scalable variational procedure which can be applied on large networks in an online fashion via a Bayesian forgetting factor applied to sequential variational approximations to the posterior distribution. The proposed framework is tested on simulated and real-world data, and it rapidly and accurately detects changes to the latent edge process rates, and to the latent node group memberships, both in an online manner. In particular, in an application on the Santander Cycles bike-sharing network in central London, we detect changes within the network related to holiday periods and lockdown restrictions between 2019 and 2020.
Keywords: Network point process; Online variational inference; Stochastic block model; Streaming data.
© The Author(s) 2025.
Figures


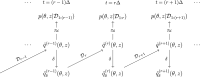








References
-
- Airoldi, E.M., Costa, T.B., Chan, S.H.: Stochastic blockmodel approximation of a graphon: theory and consistent estimation. In: Burges, C.J., Bottou, L., Welling, M., Ghahramani, Z., Weinberger, K.Q. (eds.) Advances in Neural Information Processing Systems, vol. 26. Curran Associates Inc., New York (2013)
-
- Alanqary, A., Alomar, A.O., Shah, D.: Change point detection via multivariate singular spectrum analysis. In: Beygelzimer, A., Dauphin, Y., Liang, P., Vaughan, J.W. (eds.) Advances in Neural Information Processing Systems (2021). https://openreview.net/forum?id=i0DmV60aeK
-
- Amini, A.A., Chen, A., Bickel, P.J., Levina, E.: Pseudo-likelihood methods for community detection in large sparse networks. Ann. Stat. 41(4), 2097–2122 (2013)
-
- Bifet, A., Gavaldà, R., Holmes, G., Pfahringer, B.: Machine learning for data streams: with practical examples in MOA. In: Adaptive Computation and Machine Learning series. MIT Press (2018)
-
- Bishop, C.M.: Pattern Recognition and Machine Learning (Information Science and Statistics). Springer, Berlin (2006)
LinkOut - more resources
Full Text Sources
