Topology-driven negative sampling enhances generalizability in protein-protein interaction prediction

Abstract

Motivation: Unraveling the human interactome to uncover disease-specific patterns and discover drug targets hinges on accurate protein-protein interaction (PPI) predictions. However, challenges persist in machine learning (ML) models due to a scarcity of quality hard negative samples, shortcut learning, and limited generalizability to novel proteins.

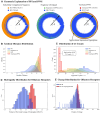
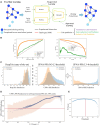
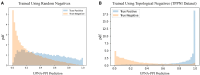
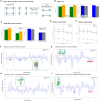
Results: In this study, we introduce a novel approach for strategic sampling of protein-protein noninteractions (PPNIs) by leveraging higher-order network characteristics that capture the inherent complementarity-driven mechanisms of PPIs. Next, we introduce Unsupervised Pre-training of Node Attributes tuned for PPI (UPNA-PPI), a high throughput sequence-to-function ML pipeline, integrating unsupervised pre-training in protein representation learning with Topological PPNI (TPPNI) samples, capable of efficiently screening billions of interactions. By using our TPPNI in training the UPNA-PPI model, we improve PPI prediction generalizability and interpretability, particularly in identifying potential binding sites locations on amino acid sequences, strengthening the prioritization of screening assays and facilitating the transferability of ML predictions across protein families and homodimers. UPNA-PPI establishes the foundation for a fundamental negative sampling methodology in graph machine learning by integrating insights from network topology.

Availability and implementation: Code and UPNA-PPI predictions are freely available at https://github.com/alxndgb/UPNA-PPI.

Figure 1.

Status quo in machine learning-based PPI prediction. (A) We observe a substantially higher number of PPI samples in the existing databases compared to PPNI samples. The lack of true negative samples is a major obstacle in training reliable machine learning models for PPI prediction. (B) Traditional machine learning training methodology utilizes random sampling from the complement graph ($G^c$) of the training PPI network (G) to obtain negative examples. However, this approach violates the closed-world assumption, i.e. not observing a PPI does not imply noninteraction between those proteins. Hence, the traditional approach fails to create high-quality PPNI and shifts the domain of learning in the loss function manifold, hampering the machine learning models from learning the true separation hyperplane between PPIs and true PPNIs. (C and D) In similarity-driven networks, entities that are alike are connected by links. For example, in social networks, people with similar interests are connected. On the other hand, in complementarity-driven networks, entities with opposing properties are linked (courtesy of Kovács et al. 2019). Nodes x and y are predicted to be connected based on $l=2$ and $l=3$ paths in (C) and (D), respectively. (E) We list six complementary properties of proteins that are major contributors to protein–protein interactions (Veselovsky et al. 2002). Leveraging the complementary nature of PPI networks has recently gained much attention and bifurcates the machine learning approaches for PPI prediction from those widely used in social network analysis.

Figure 2.

Leveraging PPI topology for PPNI sampling. (A) We propose a novel method for sampling high-quality PPNI leveraging the topology of PPI driven by its complementary nature. First, we run a traditional configuration model to identify the topologically least probable edges via entropy maximization. The bottom-N edges are then used for computing the 4-cycles or L3 paths induced by the protein pairs. (We use N = 10 million.) The configuration model helps in reducing the protein-pair search space from 156M down to 10M. Interacting pairs induce many L3 paths in the PPI network. We utilize the inverse hypothesis, namely Contrastive L3 or CL3, to filter the protein pairs from the bottom-N predictions which induce no L3 path in the PPI network. Hence, we obtain the Topological PPNI (TPPNI), which is used in the training and testing of UPNA-PPI. (B) Hyperbolic embeddings have recently been used for visualizing and link prediction tasks in complementarity-driven networks like PPI networks. We visualize the proteins involved in PPI and different PPNIs in the hyperbolic space. We observe that the proteins involved in subcellular compartmental negatives (SCN) and PPNI from the Negatome database show a large overlap with proteins in the PPI network. However, the proteins involved in TPPNI show a clear separability from the proteins in the PPI network. Proteins involved in TPPNI are toward the circumference of the hyperbolic disc and are hence constituted by evolutionarily younger proteins. (C) Lobato et al. (2018) established the relationship between the radial coordinates r of human proteins and their age by assigning proteins to six different age groups through grouping proteins based on their ancient relatives in other species (subfigure courtesy of Lobato et al. 2018). The clear selection of younger proteins by CL3 hypothesis indicates that CL3 can only identify negative interactions for younger proteins, which are less central in biological pathways. Hence, biology would optimize less competition between the complementarity mechanisms to form a biologically relevant function for younger proteins, leaving patterns in PPI topology that can distinguish younger and older proteins as captured by CL3.

Figure 3.

Geometric and chemical relevance of topological PPNI (TPPNI). (A) We visualize each PPI and PPNI in the hyperbolic space by averaging r and $\theta$ for each protein pair. TPPNI provides the best-separating hyperplane that can be learned by downstream tasks only from the secondary structure of proteins. (B) We plot the distributions of geodesic distances between the protein pairs in PPI and different PPNIs (number of samples for each type n = 2311). TPPNI identifies pairs of proteins that are significantly far from each other in the hyperbolic geometry of the human PPI network. Hence, compared to SCN and Negatome, TPPNI offers negative pairs with unique patterns, allowing ML to decode and learn such patterns. (C) We plot the L3 count distributions for PPI and various PPNIs. While the protein pairs in PPNI induce a significantly lower number of L3 paths in the PPI network, we select the pairs inducing no L3 path in the TPPNI for training and testing of UPNA-PPI. (D) The Grand Average of Hydropathy (GRAVY) is a measure of the hydrophobicity or hydrophilicity of a peptide or protein (Kyte and Doolittle 1982). The more negative the score, the more hydrophilic the amino acid is, and the more positive the score, the more hydrophobic. Humans have approximately 400 olfactory receptors (ORs), and we observed 7076 negative inter-family links among ORs in TPPNI. Also, we have 773 positive links between ORs and other proteins in our PPI; none of the 773 PPI OR links are inter-family. The distribution of the product of GRAVY scores between PPI ORs and OR–OR PPNI (randomly sampled 773 TPPNI) shows that the CL3 resulted in identifying pairs of ORs that show higher hydrophobic mismatch, and hence decrease the chance of interacting with each other. (E) Similarly, we calculated the product of charge for the 773 PPI OR links and OR–OR TPPNI (charge at pH=7). The distribution of the product of charge shows that CL3 identified inter-family OR proteins with the same sign of charge, hence repelling each other and decreasing the chance of interaction.

Figure 4.

UPNA-PPI architecture, inductive link prediction, and transfer learning. (A) UPNA-PPI architecture: UPNA-PPI embeds the protein amino acid sequences into 100D vectors using ProtVec. For each protein pair, UPNA-PPI concatenates the ProtVec embeddings and feeds them to a decoder (3-layered multi-layer perceptron). (B) UPNA-PPI achieves better performance both in terms of receiver operating characteristics and precision–recall compared to two state-of-the-art models, PPI-GNN and DeepTrio, in inductive link prediction. (C) DeepTrio predicts overlapping prediction values for the PPI and PPNI test samples. UPNA-PPI shows better separation between the predictions for PPIs and PPNIs, becoming a superior ranking tool for both PPI and PPNI. (C) Predictions at the output of DeepTrio are overlapping for the PPI and PPNI data. Hence, DeepTrio is unable to separate the predictions from PPIs versus PPNIs. UPNA-PPI trained on potential negatives from the configuration model (no CL3) shows better separation between the predictions for PPIs versus PPNIs. Finally, after introducing CL3 thresholding, UPNA-PPI shows a clear separation between the predictions for PPIs and PPNIs. (D) We computed the number of L3 simple paths between all PPI pairs to investigate if UPNA-PPI has learned the complementarity mechanisms from protein sequences. Indeed, we observe a strong Spearman’s rank correlation coefficient of 0.48 between L3 counts and UPNA-PPI predictions, indicating that the TPPNI enforced UPNA-PPI to learn complementary mechanisms that drive protein–protein interactions only from the amino acid sequences. (E) We plot the F1-score on the test dataset (first fold) by changing the binary classification threshold. We observe that the test F1-score is maximized for an optimal classification threshold $\approx 0.5$. Furthermore, in subplot (D), we observe that UPNA-PPI predicts interaction probabilities greater than the optimal interaction threshold for the majority of the experimentally validated PPIs. Similar observations are made for other folds of UPNA-PPI, and the average optimal threshold is $0.476\pm 0.049$.

Figure 5.

Comparison of UPNA-PPI predictions using random negative samples versus topological negatives. Distributions of predictions for true positives and true negatives in 1-fold of the 5-fold cross-validation datasets. Random negative samples are generated by sampling edges from the complementary graph of the PPI network, maintaining the same number of random negatives as UPNA-PPI samples in the train and validation datasets, while the test dataset remains unchanged (containing complementarity-driven hard negatives and experimental negatives from Negatome 2.0 and NVDT). The figure shows reduced separability (greater overlap) between true positives and true negatives when (A) random negatives are used compared to (B) topological negatives (TPPNI) for training and validation, indicating that the model becomes less confident in distinguishing PPIs from PPNIs.

Figure 6.

Robustness and Interpretability of UPNA-PPI. (A) Degree preserved edge swap is a widely used method to randomize graphs for studying robustness. However, since PPI networks are enriched with 4-cycles, degree preserved randomization frequently duplicates existing interactions in PPI instead of creating random edges. (B) In the robustness study, we perturb train and validation datasets while keeping the test dataset unchanged. The inductive performance of UPNA-PPI is invariant to degree-preserved randomization. (C) We replace ProtVec embeddings with 100D random vectors where the value for each dimension is randomly selected from a uniform distribution $U[0,1]$. We observe inductive performance similar to a naive Bayes classifier under such randomization, confirming that UPNA-PPI learns interactions leveraging the embeddings of the amino acid sequences. (D) We randomly remove nodes (proteins) from the training and validation datasets. We do not observe significant fluctuation in UPNA-PPI inductive performance, which confirms the ability of UPNA-PPI to learn from limited data and generalize to new proteins. (E) Similar to (D), we randomly remove edges (interactions) from the training and validation datasets. We do not observe significant fluctuation in UPNA-PPI inductive performance, which confirms the ability of UPNA-PPI to learn from limited data and generalize to new proteins. (F) We ran an ablation study on the amino acid sequence of DRD2 to identify potential trigrams where interaction takes place for creating the Drd2 homodimer. In this ablation study, each amino acid trigram is replaced with the Out-of-Vocabulary (OOV) embedding from ProtVec, while keeping the other amino acid sequence in the input of UPNA-PPI unchanged. We observe multiple valleys in the binding probability profiles. These valleys correspond to the interfeces TM4/TM5 and TM1/H8, which have been identified experimentally using Cys-crosslinking and FRET. (G) We repeat a similar process for another homodimer of transcription factor ComA. (H) and (I) We run an ablation study on two heterodimers consisting of protein pairs LIF-Gp130 and Mu-opioid receptor-NbE. The interaction locations on protein complexes LIF-Gp130 and mu-Opioid receptor-NbEHH are marked in the figures, which overlap with valleys predicted by UPNA-PPI. In all of the above scenarios, we observe that the valleys with lower standard deviation obtained from 5-folds of UPNA-PPI correspond to the true binding locations. Therefore, the valleys on which 5-fold of UPNA-PPI agree are the binding locations with a higher confidence.

Figure 7.

UPNA-PPI Predictions for G-protein coupled receptors (GPCRs). (A) We validate top and bottom self-interaction predictions for GPCRs from UPNA-PPI with AlphaFold-Multimer. We observe that AlphaFold predicts a higher number of atoms at the interaction surface and pLDDT at the surface for the top predictions compared to the bottom predictions (see Table 3), which validates the agreement between UPNA-PPI and AlphaFold. (B) Interaction network of GPCRs. From the top 100 UPNA-PPI predictions, we construct the interaction network of GPCRs. We predict 8 homodimers and 92 heterodimers involving 28 GPCR proteins. (C) Similarly, we construct a noninteraction network with the bottom 100 predictions from UPNA-PPI.