Ultra narrowband geometric-phase resonant metasurfaces

Abstract

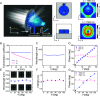
The concept of a geometric phase has sparked a revolution in photonics. Conventional space-variant polarization manipulation in optical systems only results in broadband geometric phases. Recently emerged nonlocal metasurfaces show an ability to compress the operating bandwidth through modulations of wavelength-dependent amplitudes. However, their geometric phases are still broadband and not linear, posing severe challenges to realize ultra narrowband metadevices. Here, we propose and demonstrate the generation of ultra narrowband and spatially variable geometric phases in resonant metasurfaces. We find that an array of perturbed Mie resonators is able to simultaneously preserve its global symmetry and local transformation. Local transformation provides a pixel-level geometric phase, whereas global symmetry yields an ultranarrow operation bandwidth. We further reveal that this geometric phase can be well pinned to the resonant mode by introducing additional perturbations to individually define the phase at nonresonant wavelengths. Consequently, we realize experimentally pixelated phase-gradient metasurfaces and metalenses with record-breaking Q factors and high confidentiality. We believe that our general approach and demonstrated results will open a paradigm of multiplexed metasurfaces and information encryption.

Keywords: bound state in the continuum; geometric phase; metasurface; narrow band; nonlocal metasurface.

Fig. 1.

Concept of high-Q phase-gradient metasurfaces. (A) Schematic picture of the Si metasurface. Insets show a single cell with detailed structural parameters. (B) and (C) show the dependence of resonant wavelength and Q factor of BIC mode on the radius of an air hole. (D) Resonant wavelength (Top) and FWHM (Bottom) of quasi-BIC mode as a function of rotational angle θ. Here, the size of the air hole is fixed at r = 30 nm. Insets show the numerically calculated distributions of power (Top) and electric field (Bottom). (E) Acquired geometric phase ϕ_PB (dots) as a function of rotational angle θ. The solid line represents the curve of ϕ_PB = 2θ. (F) Dependence of Q factors of supercells containing N phase steps of our metasurface (dots) and conventional nonlocal metasurface (open squares). Here, the position parameter ρ is fixed at ρ = 80 nm. The Inset shows the schematic of a conventional nonlocal metasurface structure.

Fig. 2.

Realization of ultrahigh-Q phase-gradient metasurfaces. (A) SEM image of Si metasurface. Insets are the high-resolution top-view (Top) and tilt-view SEM images. (B) Cross-polarized transmission spectrum of Si metasurface (dots) and its fitted line. (C) Experimentally recorded PB phase of Si metasurface as a function of rotation angle θ (dots). The solid line represents the ideal value of ${\mathrm{\Phi }}_{\mathit{PB}}=2\theta$. (D) and (E) are the corresponding resonant wavelength and FWHM. The lines in (D and E) are values of Si metasurfaces with pixel-variable rotation angle θ. The corresponding schematic is shown as the Inset in Fig. 2D.

Fig. 3.

Ultrahigh-Q metalens with NA = 0.18. (A) Top-view SEM of the Si Metalens. The Inset shows the phase profile in design. (B) and (C) are the experimentally recorded intensity profiles of focal spots in x-y and x-z planes at different wavelengths. (D) Measured cross-polarized intensity at the focal spot as a function of wavelength. The intensity drops dramatically with a slight wavelength detuning and a record FWHM of 1.3 nm is achieved. (E) Experimental (dots) and theoretical (line) linecuts of the focal spot at a wavelength of 1,519.3 nm.

Fig. 4.

Narrowband geometric phase. (A) The schematic of the narrowband geometric phase-based metasurface. Insets show the top-view and side-view images of unit cells and the corresponding field distribution ($E\left(x,y\right)$) at resonant and nonresonant wavelengths. (B) Transmission coefficients of x- and y-polarized incident light as a function of the bar width w. (C) and (D) show the numerically simulated resonant wavelength and the corresponding geometric phase (dots) of narrowband metasurfaces with different rotation angle θ. The open squares in (D) are the corresponding geometric phase at nonresonant wavelength for a direct comparison. (E) and (F) are experimentally recorded resonant wavelengths and FWHMs of Si metasurface with different rotation angle θ. (G) The experimentally recorded PB phases at resonant wavelength (blue dots) and nonresonant wavelength (red dots), respectively.

Fig. 5.

High-Q metalenses based on the narrowband geometric phase. (A) Top-view SEM of the Si Metalens. The Inset shows the phase profile in design. (B) Experimentally recorded intensity profiles of a focal spot in the x-y plane at different wavelengths. (C) Experimentally recorded cross-polarized intensity at the focal spot as a function of wavelength, giving an FWHM of 1.4 nm. (D) Measured cross-polarized intensity at focal spots of conventional high-Q metalens (blue dots) and metalens with narrowband PB phase (red dots) under different incident power. (E) and (F) show the focusing intensity distribution of the traditional nonlocal metalens and the nonlocal metalens with a narrowband PB phase in the x-y plane under different incident powers. The incident laser in (E and F) is fixed at a nonresonant wavelength of 1,515.1 nm. Conventional nonlocal metalenses still experience focal spots at high incident powers, while narrowband nonlocal metalenses can completely eliminate these effects.