Computation of Protein-Ligand Binding Free Energies with a Quantum Mechanics-Based Mining Minima Algorithm

Abstract

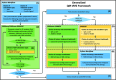
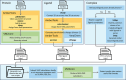
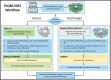
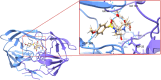
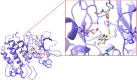
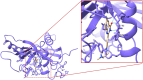
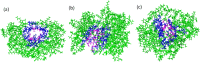
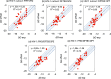
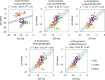
A new method, protein-ligand QM-VM2 (PLQM-VM2), to calculate protein-ligand binding free energies by combining mining minima, a statistical mechanics end-point-based approach, with quantum mechanical potentials is presented. PLQM-VM2 is described in terms of a highly flexible workflow that is initiated from a Protein Data Bank (PDB) file and a chemical structure data file (SD file) containing two-dimensional (2D) or three-dimensional (3D) ligand series coordinates. The workflow utilizes the previously developed molecular mechanics (MM) implementation of the second-generation mining minima method, MM-VM2, to provide ensembles of protein, free ligand, and protein-ligand conformers, which are postprocessed at chosen levels of QM theory, via the quantum chemistry software package GAMESS, to correct MM-based conformer geometries and electronic energies. The corrected energies are used in the calculation of configuration integrals, which on summation over the conformer ensembles give QM-corrected chemical potentials and ultimately QM-corrected binding free energies. In this work, PLQM-VM2 is applied to three benchmark protein-ligand series: HIV-1 protease/38 ligands, c-Met/24 ligands, and TNKS2/27 ligands. QM corrections are carried out at the semiempirical third-order density functional tight-binding level of theory, augmented with dispersion and damping corrections (DFTB3-D3(BJ)H). Bulk solvation effects are accounted for with the conductor-like polarizable continuum model (PCM). DFTB3-D3(BJ)H/PCM single-point energy-only and geometry optimization QM corrections are carried out in conjunction with two different models that address the large computational scaling associated with protein-sized molecular systems. One is a protein cutout model, whereby a set of protein atoms in and around the binding site are carved out, dangling bonds are capped with hydrogens, and only atoms directly in the protein binding site are mobile along with the ligand atoms. The other model is the Fragment Molecular Orbital (FMO) method, which includes the whole protein system but again only allows the binding site and ligand atoms to be mobile. All four of these methodological approaches to QM corrections provide significant improvement over MM-VM2 in terms of rank order and parametric linear correlation with experimentally determined binding affinities. Overall, FMO with geometry optimizations performed the best, but the much cheaper cutout single-point energy approach still provides a good level of accuracy. Furthermore, a clear result is that the PLQM-VM2 calculated binding free energies for the three diverse test systems in this work are, in contrast to those calculated using MM-VM2, directly comparable in energy scale. This suggests a basis for future development of a PLQM-VM2-based multiprotein screening capability to check for off-target activity of ligand series. Benchmark timings on a single compute node (32 CPU cores) for PLQM-VM2 calculation of the chemical potential of a protein-ligand complex range from ca. 30-45 min for the single-point energy approaches to ∼5 h for the cutout approach with geometry optimization and to ∼35 h for the full protein FMO approach with geometry optimization.

Figure 1

Generalized framework for QM-VM2. Blue indicates steps carried out by the VeraChem Python workflow. Green and yellow indicate calculations driven by the individual VM2core and GAMESS packages, respectively, while green/yellow gradient indicates calculations carried out by the combined VM2core-GAMESS package. Abbreviations used in the figure are defined as follows: VM2: Carry out iterative mining minima free energy calculation including conformational searching; feprocess: skip conformational search and calculate configuration integrals only for supplied starting conformers; SPE: single-point energy correction at chosen theory level; OPT: geometry optimization at chosen theory level; cutout: for proteins (or other large receptors) include only the area in and around the binding site in the calculation; fragmentation: for proteins (or other large receptors) use a fragmentation QM method.

Figure 2

Flow diagram depicting the MM-VM2 workflow for the calculation of protein–ligand binding free energies. Blue portions indicate steps carried out by the VeraChem Python workflow code, green portions indicate steps carried out by the VM2core executable, and yellow portions indicate steps carried out by AmberTools.

Figure 3

Flow diagram of PLQM-VM2 with the cutout and full protein approaches applied in this work. Blue portions indicate steps carried out by the VeraChem Python workflow code, green portions indicate steps carried out by the VM2core executable, yellow portions indicate steps carried out by GAMESS, and gray portions indicate steps carried out by fragmentation programs. Green/yellow gradients are steps carried out by the combined VM2core-GAMESS executable. Note that, while not applied in the current work, the implemented generalized QM-VM2 framework (Figure 1) allows for the combination of the cutout and fragmentation approaches.

Figure 4

HIV-1-protease structure with bound ligand 21e/AD-81 (Table 1) and the protein–ligand bridging flap water. For the ligand, noncarbon atoms are represented by different colors: nitrogen (blue), oxygen (red), sulfur (yellow), chlorine (green), and hydrogen (white). Protein residues that have significant interactions with the ligand are labeled in the figure.

Figure 5

c-Met protein structure with bound inhibitor lig63 (Table 2). For the ligand, noncarbon atoms are represented by different colors: nitrogen (blue), oxygen (red), sulfur (yellow) chlorine (green), and hydrogen (white). The c-Met residues MET 150 and TYR 169 are colored purple and light blue, respectively.

Figure 6

TNKS2 protein structure with bound ligand 8a (Table 3). For the ligand, noncarbon atoms are represented by different colors: nitrogen (blue), oxygen (red), sulfur (yellow), chlorine (green), and hydrogen (white). Protein residues with significant interactions with the ligand are labeled in the figure.

Figure 7

Protein cutout model depictions for (a) HIV-1 protease, (b) c-Met, and (c) TNKS2, where magenta represents “live” (mobile) regions, magenta plus blue represents the “real” region (i.e., atoms that are included in energy calculations), and green represents protein regions that are excluded from protein cutout calculations.

Figure 8

Comparison of calculated vs experimental binding free energies of the HIV-1 protease protein system using (a) MM-VM2, (b) cutout/DFTB3 SPE, (c) cutout/DFTB3, (d) FMO/DFTB3 SPE, and (e) FMO/DFTB3 OPT. The regions of 1 and 2 kcal/mol deviations from experiment are indicated by dash and dot diagonal lines, respectively. The solid blue line corresponds to the ideal linear fit.

Figure 9

Comparison of calculated vs experimentally measured binding free energies of the c-Met protein system using (a) MM-VM2, (b) cutout/DFTB3 single-point energy (SPE), (c) cutout/DFTB3 optimization (OPT), (d) FMO/DFTB3 single-point energy (SPE), and (e) FMO/DFTB3 optimization (OPT). While all data are represented in orange, the data for lig41, lig42, and lig63 are highlighted in green. The linear regression equations of the full system and the data excluding lig41, lig42, and lig63 are shown in black and pink, respectively. The regions of 1 and 2 kcal/mol deviations from experiment are indicated by dash and dot diagonal lines, respectively. The solid blue line corresponds to the ideal linear fit.

Figure 10

Graphs of calculated vs experimentally measured binding free energies of the TNKS2 protein system for: (a) MM-VM2, (b) cutout/DFTB3 single-point energy, (c) cutout/DFTB3 optimization, (d) FMO/DFTB3 single-point energy, and (e) FMO/DFTB3 optimization. While the black equation is the linear regression of the full system, orange and green are those of the split data for charge = 0 and charge = 1, respectively. The regions of 1 and 2 kcal/mol deviations from experiment are indicated by dash and dot diagonal lines, respectively. The solid blue line corresponds to the ideal linear fit.

Figure 11

Comparison of calculated vs experimental binding free energies of the combined three protein systems using (a) MM-VM2, (b) cutout/DFTB3 SPE, (c) cutout/DFTB3, (d) FMO/DFTB3 SPE, and (e) FMO/DFTB3 OPT. The regions of 1 and 2 kcal/mol deviations from experiment are indicated by dash and dot diagonal lines, respectively. The solid blue line corresponds to the ideal linear fit. Orange, purple, and green represent the scatter plots of HIV-1, c-Met, and TNKS2, whereas the linear regression equations of each method are obtained from all three proteins.