The Riemannian Means Field Classifier for EEG-Based BCI Data

Abstract

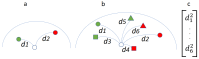
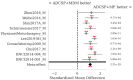
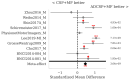
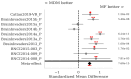
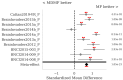
: A substantial amount of research has demonstrated the robustness and accuracy of the Riemannian minimum distance to mean (MDM) classifier for all kinds of EEG-based brain-computer interfaces (BCIs). This classifier is simple, fully deterministic, robust to noise, computationally efficient, and prone to transfer learning. Its training is very simple, requiring just the computation of a geometric mean of a symmetric positive-definite (SPD) matrix per class. We propose an improvement of the MDM involving a number of power means of SPD matrices instead of the sole geometric mean. By the analysis of 20 public databases, 10 for the motor-imagery BCI paradigm and 10 for the P300 BCI paradigm, comprising 587 individuals in total, we show that the proposed classifier clearly outperforms the MDM, approaching the state-of-the art in terms of performance while retaining the simplicity and the deterministic behavior. In order to promote reproducible research, our code will be released as open source.

Keywords: BCI; EEG; P300; Riemannian geometry; classification; motor imagery.

Figure 1

Schematic representation of the operation of the MDM, MDMF, and MF algorithms on the manifold of positive-definite matrices for a two-class problem. (a) MDM algorithm; the colored disks represent the geometric means for the two classes (red and green) as learned during the training phase. The circle is an unlabeled trial to be classified. The curves joining the disks and the circle represent the distances between them along geodesics. In this example, the trial would be classified as belonging to the green class as distance d₁ is the shortest. (b) Similar to (a), but employing a mean field composed of three power means per class. The MDMF [20] classifies the trial as belonging to the red class, as now distance d₄ is the shortest. (c) The MF submits the feature vector comprising the square of the distances d₁ to d₆ to a classifier that has been trained along with the power means. While the MDMF must classify using the minimum of all distances, the MF can learn any complex function thereof. For all three algorithms, the operation is the same for any number of classes and any number of power means per class.

Figure 2

MI data: standardized mean differences (grey diamonds) with 95% confidence interval (grey horizontal lines) and p-values per database. The comparison concerns the MF with ADCSP and the MDM with ADCSP pipelines. A positive SMD value indicates that the algorithm on the right is better and the opposite if the value is negative. The closer the SMD is to zero, the lower the effect size. The p-values for the statistical test described in Section 2.3 are shown in the right column. If significant, one, two, or three red dots indicate a p-value < 0.05, <0.01, or <0.001, respectively. The meta-effect at the bottom of the figure combines the SMD and p-values across all databases.

Figure 3

MI data: comparison of the MF and MDMF pipeline, both with ADCSP. See Figure 2 for the legend.

Figure 4

MI data: comparison of the MF with ADCSP and TS + LR with ACSTP pipeline. See Figure 2 for the legend.

Figure 5

MI data: comparison of the MF pipeline, with ADCSP and the standard CSP. See Figure 2 for the legend. For BNCI2014-001, the results are identical, consequently resulting in an effect size of zero.

Figure 6

MI data: comparison of the MF with ADCSP, with and without RPME. See Figure 2 for the legend.

Figure 7

P300 data: comparison of the proposed MF to the MDM, both with Xdawn. See Figure 2 for the legend.

Figure 8

P300 data: comparison of the proposed MF to the MDMF pipelines, both with Xdawn. See Figure 2 for the legend.

Figure 9

P300 data: comparison of the proposed MF to the golden-standard TS + LR pipelines, both with Xdawn. See Figure 2 for the legend.

Figure 10

P300 data: comparison of the proposed MF pipeline with Xdawn, with and without RPME. See Figure 2 for the legend.