A quantum mechanics-based framework for infectious disease modeling

Abstract

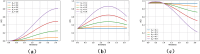
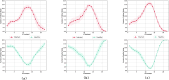
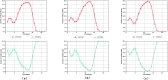
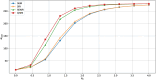
Traditional infectious disease models often use fixed compartments to represent different states of individuals. However, these models can be limited in accurately reflecting real-world conditions of individuals. In this study, we integrate quantum mechanics into infectious disease modeling, developing a quantum mechanics-based model that effectively addresses the limitations of traditional compartmental models and introduces a novel approach to understanding disease dynamics. Firstly, we examined the individual infection process and the model's evolutionary dynamics, deriving both the disease-free equilibrium point and the model's basic reproduction number. Secondly, the proposed model is simulated on a quantum circuit. The simulation results are utilized to analyze the model's parameter sensitivity and verify its rationality. The results indicate that the model's predictions align with the general patterns of viral transmission and are capable of replicating the structural attributes of compartmental models. Finally, we apply the model to simulate the spread of COVID-19. The observed similarity between the simulated results and actual infection trends demonstrates the model's effectiveness in accurately capturing viral transmission dynamics. Comparative experiments show that the proposed model significantly improves accuracy over traditional models. By leveraging quantum mechanics, our method offers a fresh perspective in infectious disease modeling, broadening the application of quantum mechanics methodologies in understanding information propagation within the macroscopic world.

Keywords: COVID-19; Compartment model; Epidemiological modeling; Infectious disease model; Quantum mechanics; Quantum superposition.

Fig. 1

An example of a network constructed using QHIM.

Fig. 2

Infection process under increasing interaction strength . (a) ; (b) ; (c) .

Fig. 3

Self-evolution process under different parameters with .

Fig. 4

Simulation of infection propagation in a Small-World network. The parameters values are detailed in Table 3 below.

Fig. 5

Simulation of Infection Propagation in a Scale-Free Network. The parameters values are detailed in Table 4 below.

Fig. 6

Changes in total infection size with increasing .

Fig. 7

Division of states under different evolutionary processes.

Fig. 8

Simulation of various models using QHIM, the model parameters are detailed in Table 4.

Fig. 9

(a) Changes in the size of infections in California over the period May 2020–April 2021. (b) Infection simulation results for COVID-19 in California.

Fig. 10

Simulation results for four counties in California, showing the proportion of total infections and the proportion of new infections per day for each county. The parameters values are detailed in Table 8 below.

Fig. 11

Comparison of prediction accuracy under different model across the four counties in California.

Fig. 12

Comparison of prediction accuracy using different model across three infectious diseases in Henan.