Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Apr 12;15(1):12580.
doi: 10.1038/s41598-025-96737-6.

Fractional order modeling of prostate cancer with pulsed treatment and the impact of effector cell killing and cell competition

Hicham Saber  1 , Hussien Albala  2 , Tariq Aljaaidi  3 , Yousef Jawarneh  1 , Abdelkader Moumen  1 , Khaled Aldwoah  4
Affiliations

Fractional order modeling of prostate cancer with pulsed treatment and the impact of effector cell killing and cell competition

Hicham Saber et al. Sci Rep. .

Abstract

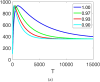
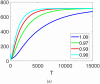
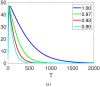
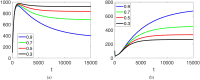
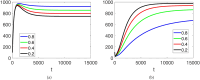
This manuscript illustrates a fractional-order mathematical model for prostate cancer (PC) growth under pulsed treatment, incorporating the effects of effector cell killing and competition between androgen-dependent (AD) and androgen-independent (AI) PC cells. We establish the existence and uniqueness of solutions using fixed-point theorems (Leray-Schauder and Banach) and investigate Ulam-Hyers stability to assess the model's solution stability under the fractional order. Numerical results are obtained via the fractional Euler method for simulation of the model at various fractional orders. Graphical results illustrate the model's dynamics, and the impact of key parameters, including the effector cell killing rate and inter-cell competition, is investigated. These findings provide insights into the complex interplay between treatment, immune response, and cancer cell dynamics, potentially informing therapeutic strategies for PC.

Keywords: Caputo operator; Euler method; Prostate cancer; Stability.

PubMed Disclaimer

Conflict of interest statement

Declarations. Competing interests: The authors declare no competing interests. Declaration of generative AI: The researchers did not use artificial intelligence in preparing this paper.

Figures

Figure 1
Figure 1
The demonstration of the state variable formula image with different values of formula image of model (2).
Figure 2
Figure 2
The demonstration of the state variable formula image with different values of formula image of model (2).
Figure 3
Figure 3
The demonstration of the state variable formula image with different values of formula image of model (2).
Figure 4
Figure 4
The demonstration of formula image on the state variables formula image and formula image with formula image of the model (2).
Figure 5
Figure 5
The demonstration of formula image on the state variables formula image and formula image with formula image of the model (2).
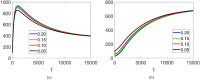
Figure 6
Figure 6
The demonstration of formula image on the state variables formula image and formula image with formula image of the model (2).
See this image and copyright information in PMC

Similar articles

See all similar articles

References

    1. Zhou, W. et al. Expression profiling of genes in androgen metabolism in androgen-independent prostate cancer cells under an androgen-deprived environment: mechanisms of castration resistance. Int. J. Clin. Exp. Pathol.9, 8424–31 (2016).
    1. Berges, R. R. et al. Implication of cell kinetic changes during the progression of human prostatic cancer. Clin. Cancer Res.1(5), 473–480 (1995). - PMC - PubMed
    1. Rutter, E. M. & Kuang, Y. Global dynamics of a model of joint hormone treatment with dendritic cell vaccine for prostate cancer. DCDS-B22(3), 1001–1021 (2017).
    1. Baez, J. & Kuang, Y. Mathematical models of androgen resistance in prostate cancer patients under intermittent androgen suppression therapy. Appl. Sci.6(11), 352 (2016).
    1. Dubey, P. & Kumar, S. Higher-order sliding mode control for androgen deprivation therapy. J. Electr. Eng. Technol.18(1), 527–537 (2023).

LinkOut - more resources