Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025;11(2):24.
doi: 10.1007/s40879-025-00816-x. Epub 2025 Apr 10.

Coarse extrinsic curvature of Riemannian submanifolds

Marc Arnaudon  1 , Xue-Mei Li  2   3 , Benedikt Petko  2
Affiliations

Coarse extrinsic curvature of Riemannian submanifolds

Marc Arnaudon et al. Eur J Math. 2025.

Abstract

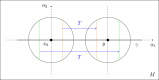
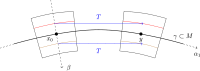
We introduce a novel concept of coarse extrinsic curvature for Riemannian submanifolds, inspired by Ollivier's notion of coarse Ricci curvature. This curvature is derived from the Wasserstein 1-distance between probability measures supported in the tubular neighborhood of a submanifold, providing new insights into the extrinsic curvature of isometrically embedded manifolds in Euclidean spaces. The framework also offers a method to approximate the mean curvature from statistical data, such as point clouds generated by a Poisson point process. This approach has potential applications in manifold learning and the study of metric embeddings, enabling the inference of geometric information from empirical data.

Keywords: Coarse curvature; Extrinsic curvature; Optimal transport.

PubMed Disclaimer

Conflict of interest statement

Competing interestsThe authors declare no competing interests.

Figures

Fig. 1
Fig. 1
Planar curve case: test measures in red with some transport pairs of T in blue (Color figure online)
Fig. 2
Fig. 2
Space curve case: test measures in red with some transport pairs of T in blue (Color figure online)
Fig. 3
Fig. 3
Fermi coordinates along γ adapted to the surface M embedded in R3
Fig. 4
Fig. 4
Test measures in red with some transport pairs of T in blue (Color figure online)
Fig. 5
Fig. 5
Top-down perspective for the transport map T
Fig. 6
Fig. 6
Cross-sectional perspective for the transport map T
See this image and copyright information in PMC

References

    1. Ambrosio, L., Gigli, N., Savaré, G.: Diffusion, optimal transport and Ricci curvature for metric measure spaces. Eur. Math. Soc. Newsl. 103, 19–28 (2017)
    1. Arnaudon, M., Li, X.M., Petko, B.: Coarse Ricci curvature of weighted Riemannian manifolds (2023). arXiv:2303.04228
    1. Boissonnat, J.-D., Guibas, L.J., Oudot, S.Y.: Manifold reconstruction in arbitrary dimensions using witness complexes. Discrete Comput. Geom. 42(1), 37–70 (2009) - PMC - PubMed
    1. Bonciocat, A.-I., Sturm, K.-T.: Mass transportation and rough curvature bounds for discrete spaces. J. Funct. Anal. 256(9), 2944–2966 (2009)
    1. Chazal, F., Cohen-Steiner, D., Lieutier, A., Mérigot, Q., Thibert, B.: Inference of curvature using tubular neighborhoods. In: Najman, L., Romon, P. (eds.) Modern Approaches to Discrete Curvature. Lecture Notes in Mathematics, vol. 2184, pp. 133–158. Springer, Cham (2017)

LinkOut - more resources