Detection of chaotic patterns in dripping faucets through nonlinear dynamic system analysis based on observations using 2700 high-frequency frames
- PMID: 40236796
- PMCID: PMC11999285
- DOI: 10.1016/j.mex.2025.103295
Detection of chaotic patterns in dripping faucets through nonlinear dynamic system analysis based on observations using 2700 high-frequency frames
Abstract
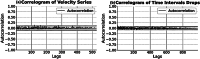
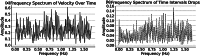
The objective of this study is the detection of chaotic patterns in the dripping of a faucet by means of nonlinear dynamical systems analysis. A controlled experiment was designed by setting up a physical system with a dripping faucet under varying conditions. High-speed cameras were used to capture video sequences and analyze the time series of the dripping under different conditions, including variations in water pressure and drip rate. The analysis included the calculation of indicators for the time series of dripping from a faucet. Thus, the 0-1 chaos test for the drip rate showed a high value (0.841), suggesting chaotic dynamics, while the Kaplan-Yorke exponent (79.935) confirms the fractal complexity of the system. Although the Kolmogorov-Sinai entropy did not evidence strictly chaotic behavior, the analysis of the Lyapunov exponent (-0.0136) points to the presence of moderate stability under certain conditions. These results, combined with the high complexities observed in the permutation entropy (0.893) and the nonlinear dynamics of the system, suggest that the tap drip under specific conditions can be modeled as a chaotic dynamical system. These findings are relevant in the study of nonlinear dynamics in hydraulic systems related to the modeling of chaotic systems in engineering and applied physics do is to find evidence of self-organization in hydraulic geometry.•The experimental behavior of the dripping faucet demonstrates nonlinear dynamics suggesting underlying complexity and possible chaotic patterns in the system flow.•The observed dynamics highlight the importance of studying drip systems to better understand and model the intricate behavior of hydraulic flows under controlled conditions.•This analysis provides insight into the chaotic tendencies of drip systems, which could have broader implications for understanding and predicting nonlinear behaviors in hydraulic and physical systems.
Keywords: Chaotic patterns; Dripping faucet; Experimental observations; High-frequency analysis; Method to establish the presence of chaos is a non-linear dynamic system; Nonlinear dynamics; Permutation entropy.
© 2025 The Author(s).
Conflict of interest statement
The author declares that there are no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Figures




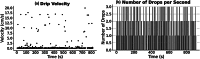





References
-
- Fuchikami N., Ishiokay S., Kiyono K. «Chaotic dynamics of a dripping water faucet,». Simul. Drip. Faucet. 2023 doi: 10.48550/arXiv.2307.05484. n°. - DOI
-
- H. Suetani, K. Soejima, R. Matsuoka, y U. Parlitz, «Manifold learning approach for Chaos in the Dripping Faucet,» arXiv, n° https://arxiv.org/abs/1205.5149, p. 1205.5149, 2012. - PubMed
-
- P. Coullet, L. Mahadevany . C.S. Riera, «Hydro-dynamical models for the chaotic dripping faucet,» arXiv, n° https://arxiv.org/abs/physics/0408096, 2004.
LinkOut - more resources
Full Text Sources
Miscellaneous

