Meta-frequency modulation in LQR vibration control with chirp excitation

Abstract

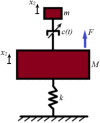
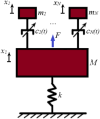
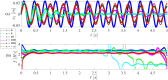
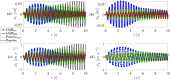
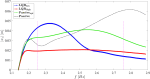
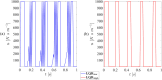
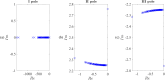
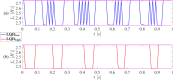
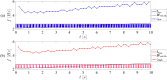
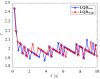
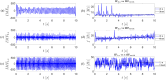
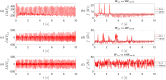
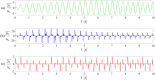
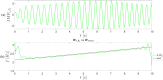
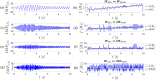
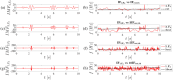
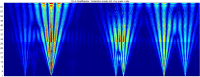
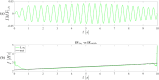
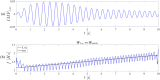
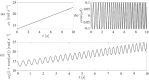
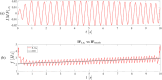
This paper presents a comprehensive analysis of the indirect control of inertial properties of a rigid bodies system by semi-actively modifying the viscosity of tunable dampers. Linear Quadratic Regulator (LQR) optimal control logic and Hilbert-Huang Transform (HHT) analysis are employed to investigate its impact on the system response. The study utilizes a simple 2-d.o.f. architecture, referred to as the Toy Model, to demonstrate how proper selection of the damping coefficient allows for manipulation of the equivalent mass and variation of the natural frequency within a specific resonant band. Chirp excitations are applied to the Toy Model, and an iterative LQR scheme is implemented to optimally control the damping coefficient, thereby preventing resonance. Given that the adoption of the semi-active controller significantly alters the primary mass response, it is crucial to establish the cause-and-effect relationship between the control law and system response, which is achieved through the HHT. Notably, the proposed model is the first known example of a physical system that exhibits both intra- and inter-wave modulations of the instantaneous frequency of the main mass response, leading to a meta-phenomenon here defined as meta-frequency modulation. This meta-frequency modulation nonlinearly distorts the response of the optimally controlled system compared to passive optimization.

Keywords: Empirical mode decomposition; Hilbert transform; Inter-wave; Intra-wave; Linear quadratic regulator.

Fig. 1

Toy Model architecture with a single small auxiliary mass-damper device.

Fig. 2

Toy Model architecture with several small auxiliary mass-damper devices.

Fig. 3

In (a) the response of the Toy model excited by an impulse of velocity for different damping coefficient values and in (b) the corresponding IFs.

Fig. 4

FRF of the Toy Model system.

Fig. 5

Comparison between LQR controlled solutions (blue and red lines) and the optimized (green line) and non-optimized (black dotted line) passive solutions for the main mass in (a)–(c), and for the auxiliary mass in (b)–(d).

Fig. 6

Comparison between the displacements amplitudes of the LQR controlled responses and the optimized and non-optimized passive responses of the main mass with respect to the resonant band (magenta dotted lines) of the Toy Model system.

Fig. 7

Optimal damping coefficient control laws for the LQR_low in (a) and LQR_high settings in (b) (focus over 1 s-window).

Fig. 8

In (a) I pole, in (b) II pole and in (c) III pole of the TF of the Toy Model system computed by substituting the optimal damping coefficient control law produced by the LQR_low setting.

Fig. 9

Current resonant frequency of the Toy Model system corresponding to the LQR_low in (a) and LQR_high settings in (b) (focus over 1 s-window).

Fig. 10

Comparison between the control frequency , the current resonant frequency of the Toy Model system and the of the chirp excitation for the LQR_low in (a) and LQR_high settings in (b).

Fig. 11

Ratio between the characteristic frequency and the of the chirp excitation for the LQR_low and LQR_high settings.

Fig. 12

In (a)–(c)–(e) main IMFs and in (b)–(d)–(f) corresponding IFs obtained from the application of the HHT to the optimal damping coefficient coming from the LQR_low setting (i, u and j∙ext in the legend of subfigures (b)–(d)–(f) stand for IF_{i, u} and j∙IF_ext,th and so on).

Fig. 13

In (a)–(c)–(e) main IMFs and in (b)–(d)–(f) corresponding IFs obtained from the application of the HHT to the optimal damping coefficient coming from the LQR_high setting (i, u and j∙ext in the legend of subfigures (b)–(d)–(f) stand for IF_{i, u} and j∙IF_ext,th and so on).

Fig. 14

Comparison between: (a) the damping force corresponding to the optimized passive setting (green) and the control damping forces coming from LQR_low (blue) in (b) and LQR_high (red) settings (c).

Fig. 15

In (a) main IMF and in (b) corresponding IF associated with the damping force coming from the optimized passive setting.

Fig. 16

In (a)–(c)–(e)–(g) main IMFs and in (b)–(d)–(f)–(h) corresponding IFs associated with the control damping force coming from the LQR_low setting (i, u and j∙ext in the legend of subfigures (b)–(d)–(f)–(h) stand for IF_{i, u} and j∙IF_ext,th and so on).

Fig. 17

In (a)–(c)–(e)–(g) main IMFs and in (b)–(d)–(f)–(h) corresponding IFs associated with the control damping force coming from the LQR_high setting (i, u and j∙ext in the legend of subfigures (b)–(d)–(f) stand for IF_{i, u} and j∙IF_ext,th and so on).

Fig. 18

Morlet WT of the control damping force coming from the LQR_high setting.

Fig. 19

In (a) main IMF and in (b) corresponding IF associated with the displacement response of the main mass obtained for the optimized passive setting.

Fig. 20

In (a) main IMF and in (b) corresponding IF associated with the displacement response of the main mass obtained for the LQR_low setting.

Fig. 21

Comparison between the analytical model wave in and the corresponding IMF in (a) together with the comparison between the analytical instantaneous frequency and the IF associated with the IMF of in (b).

Fig. 22

In (a)–(b) the main features of and in (c) their resulting contribute.

Fig. 23

In (a) main IMF and in (b) corresponding IF associated with the displacement response of the main mass obtained for the LQR_high setting.

Fig. 24

Experimental setup.

Fig. 25

Experimental flowchart.